
【题目】我们定义:如图1,在![]() 中,把AB绕点A顺时针旋转
中,把AB绕点A顺时针旋转![]() 得到
得到![]() ,把AC绕点A逆时针旋转
,把AC绕点A逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() 当
当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”, ![]() 边
边![]() 上的中线AD叫做
上的中线AD叫做![]() 的“旋补中线”,点A叫做“旋补中心”.
的“旋补中线”,点A叫做“旋补中心”.
特例感知:
![]() 在图2,图3中,
在图2,图3中,![]() 是
是![]() 的“旋补三角形”,AD是
的“旋补三角形”,AD是![]() 的“旋补中线”.
的“旋补中线”.
![]() 如图2,当
如图2,当![]() 为等边三角形时,AD与BC的数量关系为
为等边三角形时,AD与BC的数量关系为![]() ______BC;
______BC;
![]() 如图3,当
如图3,当![]() ,
,![]() 时,则AD长为______.
时,则AD长为______.
猜想论证:
![]() 在图1中,当
在图1中,当![]() 为任意三角形时,猜想AD与BC的数量关系,并给予证明.
为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
![]() 如图4,在四边形ABCD,
如图4,在四边形ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在四边形内部是否存在点P,使
在四边形内部是否存在点P,使![]() 是
是![]() 的“旋补三角形”?若存在,给予证明,并求
的“旋补三角形”?若存在,给予证明,并求![]() 的“旋补中线”长;若不存在,说明理由.
的“旋补中线”长;若不存在,说明理由.

【答案】(1)①![]() ;②4;(2)结论:
;②4;(2)结论:![]() .详见解析;(3)
.详见解析;(3)![]() 的“旋补中线”长
的“旋补中线”长![]() .
.
【解析】
(1)①首先证明![]() 是含有
是含有![]() 是直角三角形,可得
是直角三角形,可得![]() 即可解决问题;②首先证明
即可解决问题;②首先证明![]() ≌
≌![]() ,根据直角三角形斜边中线定理即可解决问题;(2)结论:
,根据直角三角形斜边中线定理即可解决问题;(2)结论:![]() 如图1中,延长AD到M,使得
如图1中,延长AD到M,使得![]() ,连接
,连接![]() ,
,![]() ,首先证明四边形
,首先证明四边形![]() 是平行四边形,再证明
是平行四边形,再证明![]() ≌
≌![]() ,即可解决问题;(3)存在
,即可解决问题;(3)存在![]() 如图4中,延长AD交BC的延长线于M,作
如图4中,延长AD交BC的延长线于M,作![]() 于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作
于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作![]() 的中线
的中线![]() 连接DF交PC于
连接DF交PC于![]() 想办法证明
想办法证明![]() ,
,![]() ,再证明
,再证明![]() ,即可得出结论.
,即可得出结论.
(1)①如图2中,
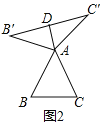
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为![]() .
.
②如图3中,
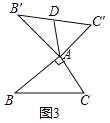
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故答案为4.
![]() 结论:
结论:![]() .
.
理由:如图1中,延长AD到M,使得![]() ,连接
,连接![]() ,
,![]()
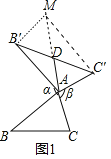
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.
![]() 存在.
存在.
理由:如图4中,延长AD交BC的延长线于M,作![]() 于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作
于E,作线段BC的垂直平分线交BE于P,交BC于F,连接PA、PD、PC,作![]() 的中线PN.
的中线PN.
连接DF交PC于O.

![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]()
易证![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形CDPF是矩形,
四边形CDPF是矩形,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,
![]() .
.
![]() 的“旋补中线”长
的“旋补中线”长![]() .
.


 能力评价系列答案
能力评价系列答案科目:初中数学 来源: 题型:
【题目】四张扑克牌的牌面如图1,将扑克牌洗匀后,如图2背面朝上放置在桌面上,小明和小亮设计了A、B两种游戏方案:
方案A:随机抽一张扑克牌,牌面数字为5时小明获胜;否则小亮获胜.
方案B:随机同时抽取两张扑克牌,两张牌面数字之和为偶数时,小明获胜;否则小亮获胜.
请你帮小亮选择其中一种方案,使他获胜的可能性较大,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D为等腰直角△ABC内一点,∠ACB=90°,AD=BD,∠BAD=30°,E为AD延长线上的一点,且CE=CA,若点M在DE上,且DC=DM.则下列结论中:①∠ADB=120°;②△ADC≌△BDC;③线段DC所在的直线垂直平分线AB;④ME=BD;正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=3,BC=4,点D在边BC上,以AD为折痕将△ABD折叠得到△AB’D,AB'与边BC交于点E.若△DEB’为直角三角形,则BD的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(2,3)且AO=BO,∠AOB=90°则点B的坐标为( )

A.(2,3)B.(-3,2)C.(-3,-2)D.(-2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1) 求![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2) 商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P为等边△ABC的边AB上一点,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于
点D.

(1)证明:PD=DQ.
(2)如图2,过P作PE⊥AC于E,若AB=2,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com