
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
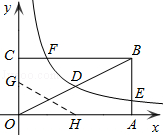
【答案】(1)2
y=![]() ,n=
,n=![]() ;
;
OG=![]() .
.
【解析】(1)∵点E(4,n)在边AB上,
∴OA=4,
在Rt△AOB中,∵tan∠BOA=![]() ,
,
∴AB=OA×tan∠BOA=4×![]() =2;
=2;
(2)根据(1),可得点B的坐标为(4,2),
∵点D为OB的中点,
∴点D(2,1)
∴![]() =1,
=1,
解得k=2,
∴反比例函数解析式为y=![]() ,
,
又∵点E(4,n)在反比例函数图象上,
∴![]() =n,
=n,
解得n=![]() ;
;
(3)如图,设点F(a,2),
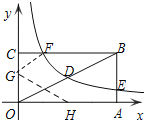
∵反比例函数的图象与矩形的边BC交于点F,
∴![]() =2,
=2,
解得a=1,
∴CF=1,
连接FG,设OG=t,则OG=FG=t,CG=2﹣t,
在Rt△CGF中,GF2=CF2+CG2,
即t2=(2﹣t)2+12,
解得t=![]() ,
,
∴OG=t=![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A旋转至△ADE的位置,使点E落在BC边上,则对于结论:①DE=BC;②∠EAC=∠DAB;③EA平分∠DEC;④若DE∥AC,则∠DEB=60°;其中正确结论的个数是( )
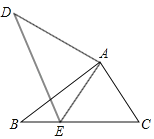
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市空气质量整治领导小组近期提出“保护好环境,拒绝冒黑烟”.某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能的公交车10辆.若购买
型两种环保节能的公交车10辆.若购买![]() 型公交车1辆,
型公交车1辆,![]() 型公交车2辆,共需400万元;若购买
型公交车2辆,共需400万元;若购买![]() 型公交车2辆,
型公交车2辆,![]() 型公交车1辆,共需350万元.
型公交车1辆,共需350万元.
(1)求购买![]() 型和
型和![]() 型公交车每辆各需多少万元?
型公交车每辆各需多少万元?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买
型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
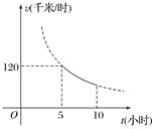
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
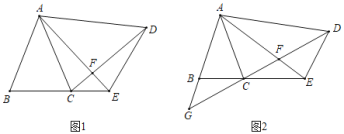
(1)求证:BE=CD.
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com