
【题目】如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
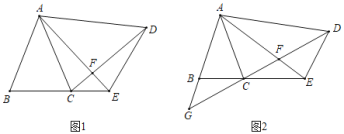
(1)求证:BE=CD.
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
【答案】(1)见解析;(2)△ACF是等腰三角形,△ADG是等腰三角形,△DEF是等腰三角形,△ECD是等腰三角形.
【解析】
(1)由“SAS”可证△ACD≌△ABE,可得BE=CD;
(2)如图2,图形中有四个等腰三角形:分别是①△ACF是等腰三角形,②△ADG是等腰三角形,③△DEF是等腰三角形;④△ECD是等腰三角形;根据已知角的度数依次计算各角的度数,根据两个角相等的三角形是等腰三角形得出结论.
解:(1)如图1,∵∠BAC=∠EAD,
∴∠BAC+∠CAE=∠EAD+∠CAE,
即∠BAE=∠CAD,且AB=AC,AD=AE,
∴△ACD≌△ABE(SAS)
∴BE=CD;
(2)如图2,
①∵∠BAC=∠EAD=30°,
∴∠ABC=∠ACB=∠AED=∠ADE=75°,
由(1)得:∠ACD=∠ABC=75°,
∠DCE=∠BAC=30°,
∵AD⊥AB,
∴∠BAD=90°,
∴∠CAE=30°,
∴∠AFC=180°﹣30°﹣75°=75°,
∴∠ACF=∠AFC,
∴△ACF是等腰三角形,
②∵∠BCG=∠DCE=30°,∠ABC=75°,
∴∠G=45°,
在Rt△AGD中,∠ADG=45°,
∴△ADG是等腰三角形,
③∠EDF=75°﹣45°=30°,
∴∠DEF=∠DFE=75°,
∴△DEF是等腰三角形;
④∵∠ECD=∠EDC=30°,
∴△ECD是等腰三角形.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E且AB=AE,延长AB与DE的延长线相交于点F,连接AC、CF.下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③BF=AD;④S△BEF=S△ABC;⑤S△CEF=S△ABE;其中正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() (x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,
(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,![]() =________.
=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
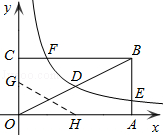
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐角系中,点![]() 是原点,点
是原点,点![]() 、
、![]() 在坐标轴上,连接
在坐标轴上,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且点
轴上,且点![]() 是线段
是线段![]() 的垂直平分线上一点.
的垂直平分线上一点.
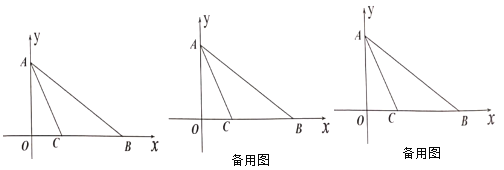
(1)求点![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发以每秒2个单位长度的速度向终点
出发以每秒2个单位长度的速度向终点![]() 运动(点
运动(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 、
、![]() ,若点
,若点![]() 的运动时间为
的运动时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的条件下,过点![]() 作
作![]() 垂直
垂直![]() 轴,交
轴,交![]() 于
于![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)abc>0;(3)b2-4ac>0;(4)5a+c=0;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有______(填序号).
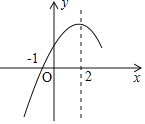
查看答案和解析>>
科目:初中数学 来源: 题型:
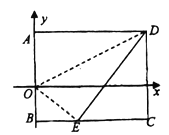
【题目】如图,将矩形纸片![]() 放入以
放入以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 边上一点
边上一点![]() 为坐标原点的直角坐标系中,连接
为坐标原点的直角坐标系中,连接![]() .将纸片
.将纸片![]() 沿
沿![]() 折叠,使得点
折叠,使得点![]() 落在
落在![]() 边上点
边上点![]() 处,若
处,若![]() ,
,![]() ,在
,在![]() 上存在点
上存在点![]() ,使
,使![]() 到
到![]() 、
、![]() 的距离之和最小,则点
的距离之和最小,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店销售一批运动鞋,零售价每双240元.如果一次购买超过10双,那么每多购1双,所购运动鞋单价降低6元,但单价不能低于150元.若该顾客购买了x双(x>10)这批运动鞋.
(1)设每双运动鞋的价格为y元,求y与x的函数关系式;
(2)若该顾客购买这种运动鞋支付了3600元,则该顾客买了多少双运动鞋?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com