
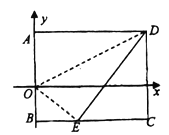
【题目】如图,将矩形纸片![]() 放入以
放入以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 边上一点
边上一点![]() 为坐标原点的直角坐标系中,连接
为坐标原点的直角坐标系中,连接![]() .将纸片
.将纸片![]() 沿
沿![]() 折叠,使得点
折叠,使得点![]() 落在
落在![]() 边上点
边上点![]() 处,若
处,若![]() ,
,![]() ,在
,在![]() 上存在点
上存在点![]() ,使
,使![]() 到
到![]() 、
、![]() 的距离之和最小,则点
的距离之和最小,则点![]() 的坐标为__________.
的坐标为__________.
【答案】(![]() ,
,![]() )
)
【解析】
连接AC交OD于F,则F到E、C的距离之和最小,由矩形的性质得出CD=AB=8,AD=BC=10,∠BCD=∠ABC=90°,由折叠的性质得出AF=EF,OA=OE,ED=AD=10,由勾股定理得出CE=6,求出BE=BCCE=4,设OA=OE=x,则OB=8x,在Rt△OBE中,由勾股定理得出方程,解方程得出OA=OE=5,得出A(0,5),D(10,5),C(10,3),由待定系数法求出直线OD和直线AC的解析式,解方程组求出两条直线的交点坐标即可.
解:连接AC交OD于F,则F到E、C的距离之和最小,
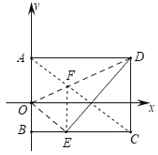
∵四边形ABCD是矩形,
∴CD=AB=8,AD=BC=10,∠BCD=∠ABC=90°,
由折叠的性质得:AF=EF,OA=OE,ED=AD=10,
∴CE=![]() ,
,
∴BE=BCCE=4,
设OA=OE=x,则OB=8x,
在Rt△OBE中,由勾股定理得:42+(8x)2=x2,
解得:x=5,
∴OA=OE=5,
∴A(0,5),D(10,5),C(10,3),
设直线OD的解析式为y=kx,
代入D(10,5)可得:5=10k,解得:![]() ,
,
∴直线OD的解析式为:y=![]() x,
x,
设直线AC的解析式为y=ax+b,
代入A,C坐标得:![]() ,解得:
,解得: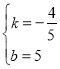 ,
,
∴直线AC的解析式为y=![]() x+5,
x+5,
解方程组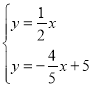 得:
得: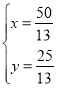 ,
,
∴点F的坐标为(![]() ,
,![]() ),
),
故答案为:(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,连接CD、AE交于点F.
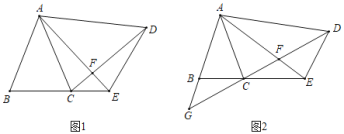
(1)求证:BE=CD.
(2)当∠BAC=∠EAD=30°,AD⊥AB时(如图2),延长DC、AB交于点G,请直接写出图中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班分成甲、乙两组进行一分钟投篮测试,并规定得6分及以上为合格,得9分及以上为优秀,现两组学生的一次测试成绩统计如下表:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组人数(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组人数(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上表数据,把下面的统计表补充完整,并写出求甲组平均分的过程;
统计量 | 平均分 | 方差 | 众数 | 中位数 | 合格率 | 优秀率 |
甲组 |
| 2.56 |
| 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 |
| 86.7% | 13.3% |
(2)如果从投篮的稳定性角度进行评价,你认为哪组成绩更好?并说明理由;
(3)小聪认为甲组成绩好于乙组,请你说出支持小聪观点的理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )

A. 1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
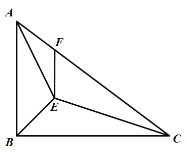
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
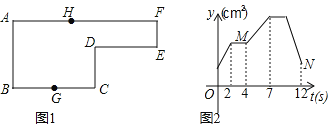
【题目】如图1,点G为BC边的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边运动,运动路径为G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列结论正确的个数有( )
①图1中BC长4cm;
②图1中DE的长是6cm;
③图2中点M表示4秒时的y值为24cm2;
④图2中的点N表示12秒时y值为15cm2.
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com