
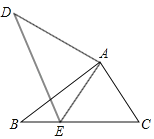
【题目】如图,将△ABC绕点A旋转至△ADE的位置,使点E落在BC边上,则对于结论:①DE=BC;②∠EAC=∠DAB;③EA平分∠DEC;④若DE∥AC,则∠DEB=60°;其中正确结论的个数是( )
A.4B.3C.2D.1
【答案】A
【解析】
由旋转的性质可知,△ABC≌△ADE,DE=BC,可得①正确;∠CAE=∠CAB﹣∠BAE,∠DAB=∠DAE﹣∠BAE,可得∠EAC=∠DAB,可判定②正确;AE=AC,则∠AEC=∠C,再由∠C=∠AED,可得∠AEC=∠AED;可判定③正确;根据平行线的性质可得可得∠C=∠BED,∠AEC=∠AED=∠C,根据平角的定义可得∠DEB=60°;综上即可得答案.
∵将△ABC绕点A旋转至△ADE的位置,使点E落在BC边上,
∴△ABC≌△ADE,
∴DE=BC,AE=AC,∠BAC=∠DAE,∠C=∠AED,故①正确;
∴∠CAE=∠CAB﹣∠BAE,∠DAB=∠DAE﹣∠BAE,
∴∠EAC=∠DAB;故②正确;
∵AE=AC,
∴∠AEC=∠C,
∴∠AEC=∠AED,
∴EA平分∠DEC;故③正确;
∵DE∥AC,
∴∠C=∠BED,
∵∠AEC=∠AED=∠C,
∴∠DEB=∠AEC=∠AED =60°,故④正确;
综上所述:正确的结论是①②③④,共4个,
故选:A.


科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E且AB=AE,延长AB与DE的延长线相交于点F,连接AC、CF.下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③BF=AD;④S△BEF=S△ABC;⑤S△CEF=S△ABE;其中正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
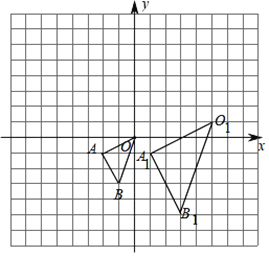
【题目】在如图所示的方格中,△O1A1B1与△OAB是关于点P为位似中心的位似图形.
(1)在图中标出位似中心P的位置,并写出点P的坐标及△O1A1B1与△OAB的位似比;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的另一个位似△OA2B2,使它与△OAB的位似比为2:1,并写出点B的对应点B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D,E分别是AB,AC的中点,延长BC至点F,使CF=![]() BC,连接CD,EF
BC,连接CD,EF
(1)求证:CD=EF;
(2)求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
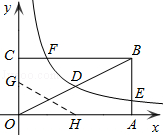
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com