
【题目】如图,等边△ABC的边长是2,D,E分别是AB,AC的中点,延长BC至点F,使CF=![]() BC,连接CD,EF
BC,连接CD,EF
(1)求证:CD=EF;
(2)求EF的长.

【答案】(1)见解析;(2)EF=![]() .
.
【解析】
(1)直接利用三角形中位线定理得出DE∥BC,DE=![]() BC,进而得出DE=FC,得出四边形CDEF是平行四边形,即可得出CD=EF;
BC,进而得出DE=FC,得出四边形CDEF是平行四边形,即可得出CD=EF;
(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理得出EF的长即可得答案.
(1)∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,DE=![]() BC,
BC,
∵使CF=![]() BC,
BC,
∴DE=FC,
∴四边形CDEF是平行四边形,
∴CD=EF.
(2)∵四边形DEFC是平行四边形,
∴CD=EF,
∵D为AB的中点,等边△ABC的边长是2,
∴AD=BD=1,CD⊥AB,BC=2,
∴EF=CD=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.
(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A旋转至△ADE的位置,使点E落在BC边上,则对于结论:①DE=BC;②∠EAC=∠DAB;③EA平分∠DEC;④若DE∥AC,则∠DEB=60°;其中正确结论的个数是( )
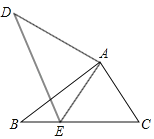
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
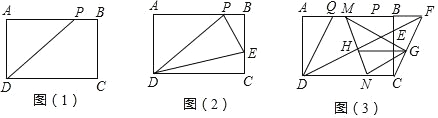
【题目】在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为![]() :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
:1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
(1)求证:PD=AB.
(2)如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当![]() 的值是多少时,△PDE 的周长最小?
的值是多少时,△PDE 的周长最小?
(3)如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作AB两种型号的环保包装盒.已知用3米同样的材料分别制成A型盒的个数比制成B型盒的个数少1个,且制作一个A型盒比制作一个B型盒要多用20%的材料.求制作每个A,B型盒各用多少材料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市空气质量整治领导小组近期提出“保护好环境,拒绝冒黑烟”.某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买![]() 型和
型和![]() 型两种环保节能的公交车10辆.若购买
型两种环保节能的公交车10辆.若购买![]() 型公交车1辆,
型公交车1辆,![]() 型公交车2辆,共需400万元;若购买
型公交车2辆,共需400万元;若购买![]() 型公交车2辆,
型公交车2辆,![]() 型公交车1辆,共需350万元.
型公交车1辆,共需350万元.
(1)求购买![]() 型和
型和![]() 型公交车每辆各需多少万元?
型公交车每辆各需多少万元?
(2)预计在该线路上![]() 型和
型和![]() 型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买
型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买![]() 型和
型和![]() 型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com