Question

【题目】如图1和2，在20×20的等距网格（每格的宽和高均是1个单位长）中，Rt△ABC从点A与点M重合的位置开始，以每秒1个单位长的速度先向下平移，当BC边与网的底部重合时，继续同样的速度向右平移，当点C与点P重合时，Rt△ABC停止移动．设运动时间为x秒，△QAC的面积为y．

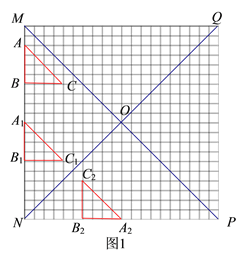
（1）如图1，当Rt△ABC向下平移到Rt△A1B1C1的位置时，请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形；

（2）如图2，在Rt△ABC向下平移的过程中，请你求出y与x的函数关系式，并说明当x分别取何值时，y取得最大值和最小值？最大值和最小值分别是多少？

（3）在Rt△ABC向右平移的过程中，请你说明当x取何值时，y取得最大值和最小值？最大值和最值分别是多少？为什么？（说明：在（3）中，将视你解答方法的创新程度，给予1～4分的加分）

Answer 1

【答案】（1）详见解析；（2）y=2x+40（0≤x≤16），当x=0时， y最小=40，当x=16时，y最大=72；（3）当x=32时， y最小=40；当x=16时， y最大=72．

【解析】试题分析：

（1）如图1，分别作出点A1、B1、C1关于直线QN的对称点A2、B2、C2，在顺次连接这三点即可得到所求三角形；

（2）如图2，当△ABC以每秒1个单位长的速度向下平移x秒时，则有：MA=x，MB=x+4，MQ=20，由题意可得：y= S梯形QMBC﹣S△AMQ﹣S△ABC，由此就可得到y与x之间的函数关系式，结合x的取值范围是即可求得y的最大值和最小值；

（3）如图2，可用如下两种方法解答本问：

方法一：当△ABC继续以每秒1个单位长的速度向右平移时，此时16≤x≤32，PB=20﹣（x﹣16）=36﹣x，PC=PB﹣4=32﹣x，由y=S梯形BAQP﹣S△CPQ﹣S△ABC即可列出y与x之间的函数关系式，结合x的取值范围即可求得y的最大值和最小值；

方法二：在△ABC自左向右平移的过程中，△QAC在每一时刻的位置都对应着（2）中△QAC某一时刻的位置，使得这样的两个三角形关于直线QN成轴对称．因此，根据轴对称的性质，只需考查△ABC在自上向下平移过程中△QAC面积的变化情况，便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况．

试题解析：

（1）如图1，△A2B2C2是△A1B1C1关于直线QN成轴对称的图形

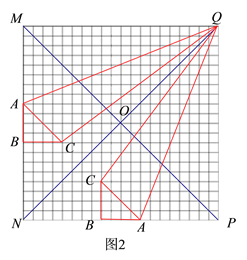
（2）当△ABC以每秒1个单位长的速度向下平移x秒时（如图2），

则有：MA=x，MB=x+4，MQ=20，

y=S梯形QMBC﹣S△AMQ﹣S△ABC

=（4+20）（x+4）﹣×20x﹣×4×4

=2x+40（0≤x≤16）．

由一次函数的性质可知：

当x=0时，y取得最小值，且y最小=40，

当x=16时，y取得最大值，且y最大=2×16+40=72；

（3）解法一：

当△ABC继续以每秒1个单位长的速度向右平移时，

此时16≤x≤32，PB=20﹣（x﹣16）=36﹣x，PC=PB﹣4=32﹣x，

∴y=S梯形BAQP﹣S△CPQ﹣S△ABC=（4+20）（36﹣x）﹣×20×（32﹣x）﹣×4×4

=﹣2x+104（16≤x≤32）．

由一次函数的性质可知：

当x=32时，y取得最小值，且y最小=﹣2×32+104=40；

当x=16时，y取得最大值，且y最大=﹣2×16+104=72．

解法二：

在△ABC自左向右平移的过程中，

△QAC在每一时刻的位置都对应着（2）中△QAC某一时刻的位置，

使得这样的两个三角形关于直线QN成轴对称．

因此，根据轴对称的性质，

只需考查△ABC在自上至下平移过程中△QAC面积的变化情况，

便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况．

当x=16时，y取得最大值，且y最大=72，

当x=32时，y取得最小值，且y最小=40．