
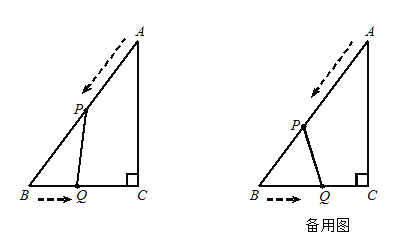
����Ŀ����ͼ����֪������y��ax2��bx��c��x�ύ��A��B���㣬��y�ύ�ڵ�C�� DΪOC���е㣬ֱ��AD���������ڵ�E��2��6��������ABE����ABC�����֮��Ϊ3��2��

��1�������������߶�Ӧ�ĺ�����ϵʽ��
��2������BD�����ж�BD��AD��λ�ù�ϵ����˵�����ɣ�
��3������BC��ֱ��AD�ڵ�M����ֱ��AD�ϣ��Ƿ���������ĵ�N�������M�غϣ���ʹ����A��B��NΪ���������������ABM���ƣ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��������ABE����ABC�����֮��Ϊ3��2��E��2��6�����ɵ�C��0��4��.
��D��0��2��. ��D��0��2����E��2��6���ɵ�ֱ��AD����Ӧ�ĺ�����ϵʽΪy��2x��2.
��y��0ʱ��2x��2��0�����x����1. ��A����1��0��.
��A����1��0����C��0��4����E��2��6����������߶�Ӧ�ĺ�����ϵʽΪ
y����x2��3x��4.
��2��BD��AD.
���B��4��0����ͨ�����ƻɶ����涨��֤����BDA��90������BD��AD.
��3����1�����M��������AM��. ����ANB�ס�ABM����������AB2��AM��AN��
��52����AN�����AN��3.�Ӷ����N��2��6��.
��2����OB��OC��4����BOC��90������ABC��45��.
��BD��AD��BD��DE��2����AEB��45��.
���AEB�ס�ABM������E������������N��2��6��.
����������1��������ABE����ABC�����֮��Ϊ3��2��E��2��6�����ɵ�C��0��4��.
��D��0��2��. ��D��0��2����E��2��6�����ݴ���ϵ�����ɵ�ֱ��AD����Ӧ�ĺ�����ϵʽΪy��2x��2.
���һ�κ�����x��Ľ�������A����1��0������A����1��0����C��0��4����E��2��6�����ݴ���ϵ����
��������߶�Ӧ�ĺ�����ϵʽΪy����x2��3x��4.
���B��4��0����ͨ�����ƻɶ����涨��֤����BDA��90������BD��AD.
����ANB�ס�ABM�����ݶ�Ӧ�߳ɱ���������õ�N�����ꡣ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
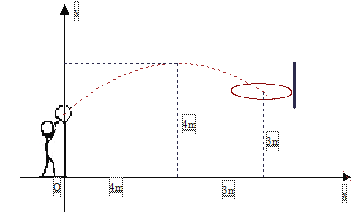
����Ŀ�������꼶��һ����������У���ͼ��Ա������Ͷ������֪�����ʱ������![]() m������Ȧ���ĵ�ˮƽ����Ϊ7m��������ֺ�ˮƽ����Ϊ4mʱ�������߶�4m�����������еĹ켣Ϊ�����ߣ���Ȧ�����3m��
m������Ȧ���ĵ�ˮƽ����Ϊ7m��������ֺ�ˮƽ����Ϊ4mʱ�������߶�4m�����������еĹ켣Ϊ�����ߣ���Ȧ�����3m��
��1��������ͼ��ʾ��ƽ��ֱ������ϵ���������ߵĽ���ʽ���жϴ����ܷ�ȷͶ�У�
��2����ʱ�����Է���Ա���ڼ�ǰ��1m�������ñ���أ���֪�ҵ��������Ϊ3.1m����ô���ܷ��óɹ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��2����20��20�ĵȾ�����ÿ��Ŀ��߾���1����λ�����У�Rt��ABC�ӵ�A���M�غϵ�λ�ÿ�ʼ����ÿ��1����λ�����ٶ�������ƽ�ƣ���BC�������ĵײ��غ�ʱ������ͬ�����ٶ�����ƽ�ƣ�����C���P�غ�ʱ��Rt��ABCֹͣ�ƶ������˶�ʱ��Ϊx�룬��QAC�����Ϊy��
��1����ͼ1����Rt��ABC����ƽ�Ƶ�Rt��A1B1C1��λ��ʱ�������������л���Rt��A1B1C1����ֱ��QN����ԳƵ�ͼ�Σ�
��2����ͼ2����Rt��ABC����ƽ�ƵĹ����У��������y��x�ĺ�����ϵʽ����˵����x�ֱ�ȡ��ֵʱ��yȡ�����ֵ����Сֵ�����ֵ����Сֵ�ֱ��Ƕ��٣�
��3����Rt��ABC����ƽ�ƵĹ����У�����˵����xȡ��ֵʱ��yȡ�����ֵ����Сֵ�����ֵ����ֵ�ֱ��Ƕ��٣�Ϊʲô����˵�����ڣ�3���У����������Ĵ��³̶ȣ�����1��4�ֵļӷ֣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���3��ѧ���������ѡ��A��B 2����깺��.
��1����ס���2��ѧ���ڲ�ͬ��깺��ĸ��ʣ�
��2����ס��ҡ���3��ѧ����ͬһ��깺��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ԡ�ABC��һ��ABΪֱ������O����O��BC�ߵĽ���Dǡ��ΪBC���е㣬����D����O�����߽�AC���ڵ�F.

��1����֤��DF��AC��
��2������ABC=30������tan��BCO��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ12���ڡ�ABC�У���C=90����AB=10cm��BC=6cm. ��P�ӵ�A��������AB����2 cm/s���ٶ����B�����ƶ�����Q�ӵ�B��������BC����1 cm/s���ٶ����C�����ƶ�. ��һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt(s).
��1����PQ��ACʱ����t��ֵ��
��2����tΪ��ֵʱ��QB=QP��
��3����tΪ��ֵʱ����PBQ���������4.8cm 2.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У��ӳ�
�У��ӳ�![]() ��
��![]() ʹ
ʹ![]() ����
����![]() ����������
Ϊ����������![]() ���ӳ�
���ӳ�![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() �ֱ���
�ֱ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��������˵������
��������˵������![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ���У� ��
��������ȷ���У� ��

A.4��B.3��C.2��D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����ϵ�У�һ�κ���y=��mx+n2����κ���y=x2+m��ͼ������ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2008��5��12�գ��봨����������8.0�����𣬸�������������˾����ʧ��ij��ѧȫ��ʦ�����������о��꼶��3����ѧ���ľ�������±���

��ʦͳ��ʱ��С�İ�īˮ�ε������������༶�ľ�����ϣ�����֪������������Ϣ��
��Ϣһ����������ľ���ܽ����7700Ԫ��
��Ϣ��������ľ���������ľ�����300Ԫ��
��Ϣ����һ��ѧ��ƽ��ÿ�˾��Ľ�����48Ԫ��С��51Ԫ��
�����������Ϣ��������ʦ�����
��1������������ľ������Ƕ���Ԫ?
��2��һ���ѧ�������Ƕ���?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com