
【题目】抛物线![]() 上部分点坐标如表所示,下列说法错误的是( )
上部分点坐标如表所示,下列说法错误的是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -6 | 0 | 4 | 6 | 6 | … |
A. 抛物线与y轴的交点为(0,6) B. 抛物线的对称轴是在y轴的右侧;
C. 抛物线一定经过点(3,0) D. 在对称轴左侧,y随x增大而减小.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,菱形
为坐标原点,菱形![]() 的对角线
的对角线![]() 在
在![]() 轴上,
轴上,![]() 两点分别在第一象限和第四象限.直线
两点分别在第一象限和第四象限.直线![]() 的解析式为
的解析式为![]() .
.

(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,![]() 为射线
为射线![]() 上一动点(不与点
上一动点(不与点![]() 和点
和点![]() 重合),过点
重合),过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() .设线段
.设线段![]() 的长度为
的长度为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)如图3,在(2)的条件下,当点![]() 运动到线段
运动到线段![]() 的延长线上时,连接
的延长线上时,连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,的角平分线
,的角平分线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3,
(1)用描点法画出y=x2+2x﹣3的图象.
(2)根据你所画的图象回答问题:当x 时,函数值y随x的增大而增大,当x 时,函数值y随x的增大而减小.
解:列表得:
X | |||||||
Y |
描点、连线

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.
(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.
(1)求甲、乙2名学生在不同书店购书的概率;
(2)求甲、乙、丙3名学生在同一书店购书的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图12,在△ABC中,∠C=90°,AB=10cm,BC=6cm. 点P从点A出发,沿AB边以2 cm/s的速度向点B匀速移动;点Q从点B出发,沿BC边以1 cm/s的速度向点C匀速移动. 当一个运动点到达终点时,另一个运动点也随之停止运动,设运动的时间为t(s).
(1)当PQ∥AC时,求t的值;
(2)当t为何值时,QB=QP;
(3)当t为何值时,△PBQ的面积等于4.8cm 2.
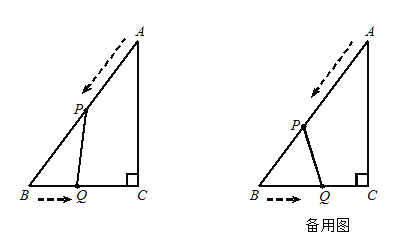
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com