
【题目】(1)计算:(![]() )×(﹣36)
)×(﹣36)
(2)计算:100÷(﹣2)2﹣(﹣2)÷(﹣![]() )
)
(3)化简:(﹣x2+3xy﹣![]() )﹣(﹣
)﹣(﹣![]() x2+4xy﹣
x2+4xy﹣![]() y2)
y2)
(4)先化简后求值:x2+(2xy﹣3y2)﹣2(x2+yx﹣2y2),其中x=﹣![]() ,y=3.
,y=3.
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元,厂方在开展促销活动期间,向客户提供两种优惠方案:
元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条(
条(![]() ).
).
(1)客户分别按方案①、方案②购买,各需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求作图,不要求写做法,但要保留作图痕迹.
(1)如图1,四边形ABCD是平行四边形,E为BC上任意一点,请只用直尺(不带刻度)在边AD上找点F,使DF=BE.

(2)如图2,BE是菱形ABCD的边AD上的高,请只用直尺(不带刻度)作出菱形ABCD的边AB上的高DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,菱形
为坐标原点,菱形![]() 的对角线
的对角线![]() 在
在![]() 轴上,
轴上,![]() 两点分别在第一象限和第四象限.直线
两点分别在第一象限和第四象限.直线![]() 的解析式为
的解析式为![]() .
.

(1)如图1,求点![]() 的坐标;
的坐标;
(2)如图2,![]() 为射线
为射线![]() 上一动点(不与点
上一动点(不与点![]() 和点
和点![]() 重合),过点
重合),过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() .设线段
.设线段![]() 的长度为
的长度为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)如图3,在(2)的条件下,当点![]() 运动到线段
运动到线段![]() 的延长线上时,连接
的延长线上时,连接![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,的角平分线
,的角平分线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
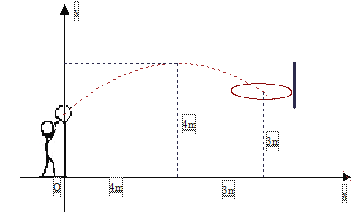
【题目】初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高![]() m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式并判断此球能否准确投中?
(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.
(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com