【题目】在平面直角坐标系中，二次函数y=x2+mx+2m﹣7的图象经过点（1，0）．

（1）求抛物线的表达式；

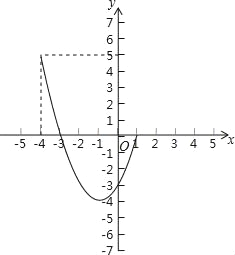
（2）把﹣4＜x＜1时的函数图象记为H，求此时函数y的取值范围；

（3）在（2）的条件下，将图象H在x轴下方的部分沿x轴翻折，图象H的其余部分保持不变，得到一个新图象M．若直线y=x+b与图象M有三个公共点，求b的取值范围．

参考答案：

【答案】（1）抛物线的表达式为y=x2+2x﹣3；

（2）y的取值范围是﹣4≤y＜5；

（3）b的取值范围是3＜b＜．

【解析】试题分析：（1）把点（1,0）代入y=x2+mx+2m﹣7即可求得m的值，从而得二次函数的解析式；（2）求出当x=﹣1时和当x=﹣4时时y的值，根据函数的增减性确定y的取值范围；（3）把抛物线y=x2+2x﹣3的图象x轴下方的部分沿x轴翻折到x轴上方，则翻折部分的抛物线解析式为y=﹣（x+1）2+4（﹣3≤x≤1），当直线y=x+b经过（﹣3，0）时，直线y=x+b与图象M有两个公共点，此时b=3；当直线y=x+b与抛物线y=﹣（x+1）2+4（﹣3≤x≤1）相切时，直线y=x+b与图象M有两个公共点，即﹣（x+1）2+4=x+b有相等的实数解，整理得x2+3x+b﹣3=0，△=32﹣4（b﹣3）=0，解得b=．结合图象可得，直线y=x+b与图象M有三个公共点，b的取值范围是3＜b＜．

试题解析：

（1）∵二次函数y=x2+mx+2m﹣7的图象经过点（1，0），

∴1+m+2m﹣7=0，解得m=2，

∴抛物线的表达式为y=x2+2x﹣3；

（2）y=x2+2x﹣3=（x+1）2﹣4，

∵当﹣4＜x＜﹣1时，y随x增大而减小；

当﹣1≤x＜1时，y随x增大而增大，

∴当x=﹣1，y最小=﹣4，

当x=﹣4时，y=5，

∴﹣4＜x＜1时，y的取值范围是﹣4≤y＜5；

（3）y=x2+2x﹣3与x轴交于点（﹣3，0），（1，0），翻折后可得新图象M如图中红色部分，

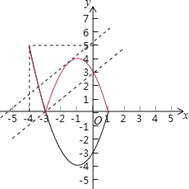
把抛物线y=x2+2x﹣3=（x+1）2﹣4的图象x轴下方的部分沿x轴翻折到x轴上方，则翻折部分的抛物线解析式为y=﹣（x+1）2+4（﹣3≤x≤1），

当直线y=x+b经过（﹣3，0）时，直线y=x+b与图象M有两个公共点，此时b=3；

当直线y=x+b与抛物线y=﹣（x+1）2+4（﹣3≤x≤1）相切时，直线y=x+b与图象M有两个公共点，

即﹣（x+1）2+4=x+b有相等的实数解，整理得x2+3x+b﹣3=0，△=32﹣4（b﹣3）=0，解得b=．

结合图象可得，直线y=x+b与图象M有三个公共点，b的取值范围是3＜b＜．

关闭