
����Ŀ����ѧϰ�˾����������֮������ͬѧ���������еĺܶ���ζ������⣬�����ǵĿα����桢A4 �Ĵ�ӡֽ�ȣ���Щ���εij����֮�ȶ�Ϊ![]() ��1�����ǽ��������������ľ��γ�Ϊ���������Ρ���ͼ��1�����ڡ��������Ρ�ABCD �У��� P Ϊ AB ���ϵĶ��㣬�� AP��AD��
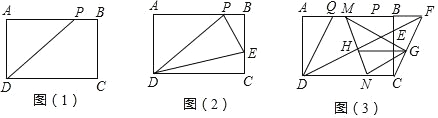
��1�����ǽ��������������ľ��γ�Ϊ���������Ρ���ͼ��1�����ڡ��������Ρ�ABCD �У��� P Ϊ AB ���ϵĶ��㣬�� AP��AD��
��1����֤��PD��AB��
��2����ͼ��2�������ڡ��������Ρ�ABCD �ı� BC ����һ���� E����![]() ��ֵ�Ƕ���ʱ����PDE ���ܳ���С��
��ֵ�Ƕ���ʱ����PDE ���ܳ���С��
��3����ͼ��3������ Q �DZ� AB �ϵĶ��㣬�� BQ��BC����֪ AD��1���ڣ�2�������������� DE ���ӳ��� AB ���ӳ����ڵ� F������ CF��G Ϊ CF ���е㣬M��N �ֱ�Ϊ�߶� QF �� CD �ϵĶ��㣬��ʼ�ձ��� QM��CN��MN �� DF �ཻ�ڵ� H������ GH �ij����Ƕ�ֵ�����ǣ����������ֵ�������ǣ���˵�����ɣ�
���𰸡���1��֤����������2��![]() ��3��
��3��![]()
��������
��1�����������������������Ķ������AD��AB������AP=AD�����ù��ɶ�����ʾ��PD�����ɵ�֤��
��2����ͼ������P����BC�ĶԳƵ�P��������DP����BC�ڵ�E����ʱ��PDE���ܳ���С����AD=PA=BC=a����ʾ��AB��CD����AB-AP��ʾ��BP���ɶԳƵ����ʵõ�BP=BP������ƽ�еñ�������������ֵ���ɣ�
��3��GH=![]() ������Ϊ���ɣ�2����֪BF=BP=AB-AP���ɵ�ʽ�����ʵõ�MF=DN������AAS�õ���MFH�ա�NDH������ȫ�������ζ�Ӧ����ȵõ�FH=DH������GΪCF�е㣬�õ�HGΪ��λ�ߣ�������λ���������GH�ij����ɣ�
������Ϊ���ɣ�2����֪BF=BP=AB-AP���ɵ�ʽ�����ʵõ�MF=DN������AAS�õ���MFH�ա�NDH������ȫ�������ζ�Ӧ����ȵõ�FH=DH������GΪCF�е㣬�õ�HGΪ��λ�ߣ�������λ���������GH�ij����ɣ�
��1����ͼ1�У���AD=BC=a������AB=CD=![]() a��
a��
���ı���ABCD�Ǿ��Σ�
���A=90�㣬
��PA=AD=BC=a��
��PD=![]() =
=![]() a��
a��
��AB=![]() a��
a��
��PD=AB��
��2����ͼ������P����BC�ĶԳƵ�P�䣬
����DP����BC�ڵ�E����ʱ��PDE���ܳ���С��
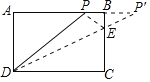
��AD=PA=BC=a������AB=CD=![]() a��
a��
��BP=AB-PA��
��BP��=BP=![]() a-a��
a-a��
��BP����CD��
��![]() ��
��
��3��GH=![]() ��������
��������
�ɣ�2����֪BF=BP=AB-AP��
��AP=AD��
��BF=AB-AD��
��BQ=BC��
��AQ=AB-BQ=AB-BC��
��BC=AD��
��AQ=AB-AD��
��BF=AQ��
��QF=BQ+BF=BQ+AQ=AB��
��AB=CD��
��QF=CD��
��QM=CN��
��QF-QM=CD-CN����MF=DN��
��MF��DN��
���NFH=��NDH��
�ڡ�MFH�͡�NDH�У�
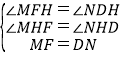 ��
��
���MFH�ա�NDH��AAS����
��FH=DH��
��GΪCF���е㣬
��GH�ǡ�CFD����λ�ߣ�
��GH=![]() CD=
CD=![]()
![]() ��2=
��2=![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
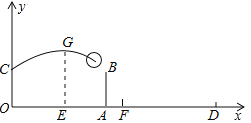
����Ŀ����ͼ����֪���ij���ODΪ18 m��λ�������ߴ������ĸ߶�ABΪ2.4 m��һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�1.6 m��C������ǰ���ɳ������������������O��ˮƽ����OEΪ6 mʱ��������ߵ�G������ͼ��ʾ��ƽ��ֱ������ϵ
(1) �������������߶�Ϊ3.4 mʱ���Է���������0.4 m�ĵ�F����һ��Ա��������������߶�Ϊ3.1 m����������Ƿ���������ɹ�����ͨ������˵��
(2) ����Ա�����Ҫ���������ֲ����߽磬��������е����߶�h��ȡֵ��Χ�Ƕ��٣�������ѹ������û���磩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����Ϊ�˽�ijС������ʹ�ù��������������ij�о�С������ɷø�С����10λ���õ���10λ����һ����ʹ�ù��������Ĵ����ֱ�Ϊ��17��12��15��20��17��0��7��26��17��9��
��1���������ݵ���λ������ ������������ ����
��2��������10λ����һ����ʹ�ù���������ƽ��������
��3������С����200�������Թ��Ƹ�С������һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AEƽ�֡�BAD����BC�ڵ�E��AB��AE���ӳ�AB��DE���ӳ����ཻ�ڵ�F������AC��CF�����н��ۣ��١�ABC�ա�EAD���ڡ�ABE�ǵȱ������Σ���BF��AD����S��BEF��S��ABC����S��CEF��S��ABE��������ȷ���У� ��

A.2��B.3��C.4��D.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
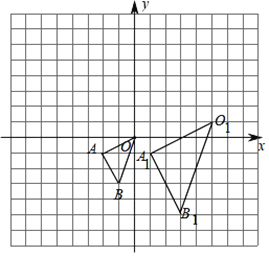
����Ŀ������ͼ��ʾ�ķ����У���O1A1B1���OAB�ǹ��ڵ�PΪλ�����ĵ�λ��ͼ�Σ�
��1����ͼ�б��λ������P��λ�ã���д����P�����꼰��O1A1B1���OAB��λ�Ʊȣ�
��2����ԭ��OΪλ�����ģ���y����Ҳ����OAB����һ��λ�ơ�OA2B2��ʹ�����OAB��λ�Ʊ�Ϊ2��1����д����B�Ķ�Ӧ��B2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
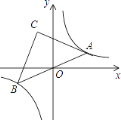
����Ŀ����ͼ���ڷ���������y= ![]() ��ͼ������һ����A������AO���ӳ���ͼ�����һ֧�ڵ�B���ڵڶ���������һ��C������AC=BC������A�˶�ʱ����Cʼ���ں���y=
��ͼ������һ����A������AO���ӳ���ͼ�����һ֧�ڵ�B���ڵڶ���������һ��C������AC=BC������A�˶�ʱ����Cʼ���ں���y= ![]() ��ͼ�����˶�����tan��CAB=2����k��ֵΪ�� ��
��ͼ�����˶�����tan��CAB=2����k��ֵΪ�� ��
A. ��3 B. ��6 C. ��9 D. ��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�ABC�ı߳���2��D��E�ֱ���AB��AC���е㣬�ӳ�BC����F��ʹCF��![]() BC������CD��EF
BC������CD��EF
��1����֤��CD��EF��
��2����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ⲻ��ʽ��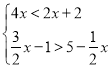 ��
��
��2���ֽ���ʽ��![]() ��
��
��3���Ȼ�������ֵ��![]() ������
������![]() ��
��
��4�����ʽ���̣�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨-1��0�����Գ���Ϊֱ��x=2�����н��ۣ���1��4a+b=0����2��abc��0����3��b2-4ac��0����4��5a+c=0����5����m��2����m��am+b����2��2a+b����������ȷ�Ľ�����______������ţ���
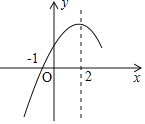
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com