
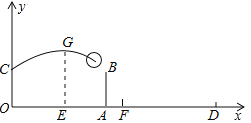
����Ŀ����ͼ����֪���ij���ODΪ18 m��λ�������ߴ������ĸ߶�ABΪ2.4 m��һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�1.6 m��C������ǰ���ɳ������������������O��ˮƽ����OEΪ6 mʱ��������ߵ�G������ͼ��ʾ��ƽ��ֱ������ϵ
(1) �������������߶�Ϊ3.4 mʱ���Է���������0.4 m�ĵ�F����һ��Ա��������������߶�Ϊ3.1 m����������Ƿ���������ɹ�����ͨ������˵��
(2) ����Ա�����Ҫ���������ֲ����߽磬��������е����߶�h��ȡֵ��Χ�Ƕ��٣�������ѹ������û���磩
���𰸡���1�����������ɹ������ɼ���������2��h��3.025
��������
��1�����ݴ�ʱ�����߶�������Ϊ��6��3.4���������ʽΪy=a��x��6��2+3.4���ٽ���C������뼴����ã��ɽ���ʽ���x=9.4ʱy��ֵ����������������߶�Ϊ3.1�ױȽϼ��ɵã�
��2���������߽���ʽΪy=a��x��6��2+h������C�������õ���h��ʾa��ʽ�ӣ��ٸ������Ҫ���������ֲ����߽缴x=9ʱ��y��2.4��x=18ʱ��y��0�ó�����h�IJ���ʽ�飬��֮���ɵã�
��1����������֪��ʱ�����ߵĶ���G������Ϊ��6��3.4����
�������߽���ʽΪy=a��x��6��2+3.4��
����C��0��1.6�����룬�ã�36a+3.4=1.6��
��ã�a=��![]() ��
��
��������еĸ߶�y��ˮƽ����x�ĺ�����ϵʽΪy=��![]() ��x��6��2+
��x��6��2+![]() ��
��
�����x=9.5ʱ��y=��![]() ��9.4��6��2+
��9.4��6��2+![]() ��2.8��3.1��
��2.8��3.1��
����������������ɹ���
��3���������߽���ʽΪy=a��x��6��2+h��
����C��0��1.6�����룬�ã�36a+h=1.6����a=![]() ��
��
���ʱ�����߽���ʽΪy=![]() ��x��6��2+h��
��x��6��2+h��
�������⣬�ã�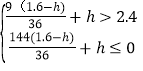 ��
��
��ã�h��3.025��
��������е����߶�h��ȡֵ��Χ��h��3.025��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������50�����乩�ο�ס�ޣ���ÿ������ķ���Ϊÿ��180Ԫʱ�������ȫ��ס������ÿ������ ÿ��ķ���ÿ����10Ԫʱ���ͻ���һ��������У���������ο;�ס��ÿ������ÿ��֧��20Ԫ�ĸ��ַ��ã����ݹ涨��ÿ������ÿ��ķ��۲��ø���340Ԫ����ÿ������ķ�������xԪ��xΪ10��������������
��1����һ�충ס�ķ�����Ϊy��ֱ��д��y��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2�������һ�������ΪwԪ����w��x�ĺ�����ϵʽ��
��3��һ�충ס���ٸ�����ʱ�����ݵ����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
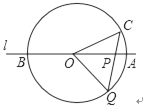
����Ŀ����ͼ��ֱ��l������O��Բ��O��������O����A��B���㣬��C����O�ϣ�����AOC=30������P��ֱ��l�ϵ�һ�����㣨��Բ��O���غϣ���ֱ��CP����O�ཻ�ڵ�Q���Ƿ���ڵ�P��ʹ��QP=QO�������ڣ������Ӧ����OCP�Ĵ�С���������ڣ����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��μ䣬��Ƥ��С��ͬѧ������ʦ�ĵ������ǰ��棬��С�ĵ�����������֮�䣬��ͼ��ʾ����һĻǡ�ɱ���ѧ��ʦ�����ˣ�����������������⣮
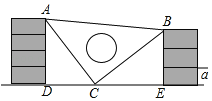
��1����֤����ADC�ա�CEB��
��2�����ÿ��ש�ĺ��a��10cm�������С��������ǰ�ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��12ax��36a��5��ͼ����4��x��5��һ��λ��x���·�����8��x��9��һ��λ��x���Ϸ�����a��ֵΪ___________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=ax2+3ax+c��a��0����y�ύ�ڵ�C����x�ύ��A��B���㣬��A�ڵ�B��࣬��B������Ϊ��1��0����C��0����3����
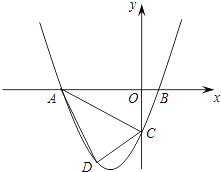
��1���������ߵĽ���ʽ��
��2������D���߶�AC�·��������ϵĶ��㣬���ı���ABCD��������ֵ��
��3������E��x���ϣ���P���������ϣ��Ƿ������A��C��E��PΪ��������ACΪһ�ߵ�ƽ���ı��Σ�����ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��2����20��20�ĵȾ�����ÿ��Ŀ��߾���1����λ�����У�Rt��ABC�ӵ�A���M�غϵ�λ�ÿ�ʼ����ÿ��1����λ�����ٶ�������ƽ�ƣ���BC�������ĵײ��غ�ʱ������ͬ�����ٶ�����ƽ�ƣ�����C���P�غ�ʱ��Rt��ABCֹͣ�ƶ������˶�ʱ��Ϊx�룬��QAC�����Ϊy��
��1����ͼ1����Rt��ABC����ƽ�Ƶ�Rt��A1B1C1��λ��ʱ�������������л���Rt��A1B1C1����ֱ��QN����ԳƵ�ͼ�Σ�
��2����ͼ2����Rt��ABC����ƽ�ƵĹ����У��������y��x�ĺ�����ϵʽ����˵����x�ֱ�ȡ��ֵʱ��yȡ�����ֵ����Сֵ�����ֵ����Сֵ�ֱ��Ƕ��٣�
��3����Rt��ABC����ƽ�ƵĹ����У�����˵����xȡ��ֵʱ��yȡ�����ֵ����Сֵ�����ֵ����ֵ�ֱ��Ƕ��٣�Ϊʲô����˵�����ڣ�3���У����������Ĵ��³̶ȣ�����1��4�ֵļӷ֣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() ����������
����������![]() �۵���ʹ��
�۵���ʹ��![]() ���
���![]() �غϣ����ۺ�
�غϣ����ۺ�![]() �ij�Ϊ�� ��
�ij��� ��
A.6B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
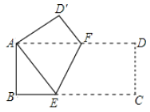
����Ŀ����ѧϰ�˾����������֮������ͬѧ���������еĺܶ���ζ������⣬�����ǵĿα����桢A4 �Ĵ�ӡֽ�ȣ���Щ���εij����֮�ȶ�Ϊ![]() ��1�����ǽ��������������ľ��γ�Ϊ���������Ρ���ͼ��1�����ڡ��������Ρ�ABCD �У��� P Ϊ AB ���ϵĶ��㣬�� AP��AD��
��1�����ǽ��������������ľ��γ�Ϊ���������Ρ���ͼ��1�����ڡ��������Ρ�ABCD �У��� P Ϊ AB ���ϵĶ��㣬�� AP��AD��
��1����֤��PD��AB��
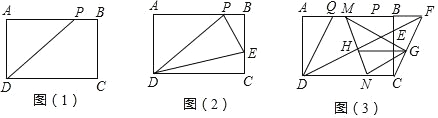
��2����ͼ��2�������ڡ��������Ρ�ABCD �ı� BC ����һ���� E����![]() ��ֵ�Ƕ���ʱ����PDE ���ܳ���С��
��ֵ�Ƕ���ʱ����PDE ���ܳ���С��
��3����ͼ��3������ Q �DZ� AB �ϵĶ��㣬�� BQ��BC����֪ AD��1���ڣ�2�������������� DE ���ӳ��� AB ���ӳ����ڵ� F������ CF��G Ϊ CF ���е㣬M��N �ֱ�Ϊ�߶� QF �� CD �ϵĶ��㣬��ʼ�ձ��� QM��CN��MN �� DF �ཻ�ڵ� H������ GH �ij����Ƕ�ֵ�����ǣ����������ֵ�������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com