
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
【答案】![]()
【解析】
根据抛物线顶点式得到对称轴为直线x=6,在4<x<5这一段位于x轴的上方,利用抛物线对称性得到抛物线在7<x<8这一段位于x轴的上方,而图象在8<x<9这一段位于x轴的下方,于是可得抛物线过点(8,0),然后把(8,0)代入y=ax2-12ax+36a-5可求出a的值.
∵抛物线y=ax12ax+36a5的对称轴为直线x=6,
而抛物线在4<x<5这一段位于x轴的下方,
∴抛物线在7<x<8这一段位于x轴的下方,
∵抛物线在8<x<9这一段位于x轴的上方,
∴抛物线过点(8,0),
把(8,0)代入y=ax12ax+36a5得64a96a+36a5=0,
解得:a= ![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.

(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是______数(填“无理”或“有理”),这个数是______;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是______;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,-5,+4,+3,-2当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3![]() ),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.
),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.

(1)请直接写出点D的坐标_____;
(2)点P在直线BC上,且△PCD是等腰直角三角形,请画出图形并求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图![]() ,在以
,在以![]() 为原点的平面直角坐标系中,抛物线
为原点的平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,
轴,![]() ,
,
![]() 求抛物线对应的二次函数的解析式;
求抛物线对应的二次函数的解析式;
![]() 若
若![]() 为抛物线
为抛物线![]() 上一动点,是否存在直线
上一动点,是否存在直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等?若存在,求出此时
的长恒相等?若存在,求出此时![]() 的值;
的值;
![]() 如图
如图![]() ,若
,若![]() 、
、![]() 为上述抛物线上的两个动点,且
为上述抛物线上的两个动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
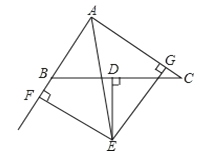
【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=![]() (AB+AC).
(AB+AC).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步促进“美丽校园”创建工作,某校团委计划对八年级五个班的文化建设进行检查,每天随机抽查一个班级,第一天从五个班级随机抽取一个进行检查,第二天从剩余的四个班级再随机抽取一个进行检查,第三天从剩余的三个班级再随机抽取一个进行检查…,以此类推,直到检查完五个班级为止,且每个班级被选中的机会均等
(1)第一天,八(1)班没有被选中的概率是 ;
(2)利用网状图或列表的方法,求前两天八(1)班被选中的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.请您确定当购买A种奖品多少件时,费用W的值最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com