
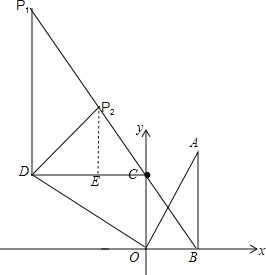
【题目】如图,Rt△ABO在平面直角坐标系中,O为原点,OB在x轴上,∠AOB=60°,点A坐标为(3,3![]() ),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.
),点C的坐标为(0,3),点D在第二象限,且△ABO≌△DCO.

(1)请直接写出点D的坐标_____;
(2)点P在直线BC上,且△PCD是等腰直角三角形,请画出图形并求点P的坐标.
【答案】(1)D(﹣3![]() ,3);(2)画图形见解析,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为(
,3);(2)画图形见解析,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为(![]() ,3+
,3+![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)由△ABO≌△DCO,利用全等三角形的性质可得CD=BA,由点A坐标为(3,3![]() ),点C的坐标为(0,3),可得D点的坐标;
),点C的坐标为(0,3),可得D点的坐标;
(2)首先利用全等三角形的性质可得OC=OB=3,∠BOC=90°,易得∠OBC=45°,分类讨论当CD为直角边时,过点D作P1D⊥CD,交BC于点P1,由DC∥OB,可得
△P1DC为等腰直角三角形,易得![]() ,可得P1点的坐标;当CD为斜边时,过D点作DP2⊥BC交BC于点P2,易得△CDP2是等腰直角三角形,作P2E⊥CD,可得CE=DE=
,可得P1点的坐标;当CD为斜边时,过D点作DP2⊥BC交BC于点P2,易得△CDP2是等腰直角三角形,作P2E⊥CD,可得CE=DE=![]() ,易得P2点的坐标.
,易得P2点的坐标.
(1)点D在第二象限,正确画出△COD如图所示,
∵△ABO≌△DCO,
∴CD=BA,
∵点A坐标为(3,3![]() ),点C的坐标为(0,3),
),点C的坐标为(0,3),
∴D(﹣3![]() ,3),
,3),
故答案为:(﹣3![]() ,3);
,3);
(2)∵OC=OB=3,∠BOC=90°,
∴∠OBC=45°,
①当CD为直角边时,如图,过点D作P1D⊥CD,交BC于点P1,
∵DC∥OB,
∴∠DCP1=∠OBC=45°,
∴△P1DC为等腰直角三角形,
∴![]() ,
,
∴P1(﹣3![]() ,3
,3![]() );
);
②当CD为斜边时,过D点作DP2⊥BC交BC于点P2,
易得△CDP2是等腰直角三角形,作P2E⊥CD,
∵CP2=DP2,
∴CE=DE=![]() ,
,
∴P2(![]() ,
,![]() )..
)..
综上所述,点P在直线BC上,使△PCD是等腰直角三角形的点P的坐标为(![]() ,3
,3![]() ),(
),(![]() ,
,![]() )..
)..


科目:初中数学 来源: 题型:
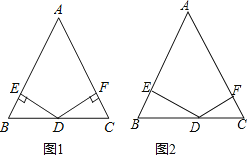
【题目】(1)如图1,等腰三角形ABC中,AB=AC,点D是BC的中点,DE⊥AB与点E、DF⊥AC与点F.求证:DE= DF;
(2)如图2,等腰三角形ABC中,AB=AC=13,BC=10,点D是BC边上的动点,DE⊥AB与点E、DF⊥AC与点F.请问DE+DF的值是否随点D位置的变化而变化?若不变,请直接写出DE+DF的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足![]() .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋节来期间,某超市以每盒80元的价格购进了1000盒月饼,第一周以每盒168元的价格销售了300盒,第二周如果单价不变,预计仍可售出300盒,该超市经理为了增加销量,决定降价,据调查,单价每降低1元,可多售出10盒,但最低每盒要赢利30元,第二周结束后,该超市将对剩余的月饼一次性赔钱甩卖,此时价格为70元/盒.
(1)若设第二周单价降低x元,则第二周的单价是 ______ ,销量是 ______ ;
(2)经两周后还剩余月饼 ______ 盒;
(3)若该超市想通过销售这批月饼获利51360元,那么第二周的单价应是多元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于![]() 的方程,并将其化成一元二次方程的一般形式.
的方程,并将其化成一元二次方程的一般形式.
(1)4个完全相同的正方形的面积之和是25,求正方形的边长![]() .
.
(2)一个矩形的长比宽多2,面积是100,求矩形的长![]() .
.
(3)一个直角三角形的斜边长为10,两条直角边相差2,求较长的直角边长![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2-12ax+36a-5的图象在4<x<5这一段位于x轴下方,在8<x<9这一段位于x轴上方,则a的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个质点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→…,若经过23秒质点到达点A,经过33秒质点到达点B,则直线AB的解析式为( )

A.y=![]() x+
x+![]() B.y=﹣
B.y=﹣![]() x+
x+![]() C.y=2x+9D.y=﹣2x+9
C.y=2x+9D.y=﹣2x+9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com