
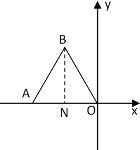
【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足![]() .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

【答案】(1)A(-4,0);(2)M(4,0);(3)OP= CD+![]() AD,证明见解析.
AD,证明见解析.
【解析】
(1)如图1中,作BN⊥AO于N.由非负数的性质求出点B坐标即可解决问题;
(2)只要证明△ABC≌△AOP,得出∠ABC=∠AOP=90°,在Rt△ABM中,解直角三角形即可解决问题;
(3)如图3中,取AD的中点R,连接BR、OR.首先证明A、B、D、O四点共圆,推出∠BAD=∠BOD=90°-60°=30°,可得BD=![]() AD,再证明△OAP≌△BAC,可得OP=BC=CD+BD=CD+
AD,再证明△OAP≌△BAC,可得OP=BC=CD+BD=CD+![]() AD.
AD.
(1)如图1中,作BN⊥AO于N.
∵![]() ,
,
∴a=-2,b=2![]() ,
,
∴B(-2,2![]() ),
),
∵BA=BO,BN⊥OA,
∴NA=NO=2,
∴OA=4,
∴A(-4,0).
(2) 如图2中,
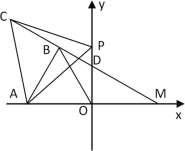
∵△ABO,△APC都是等边三角形,
∴∠OAB=∠PAC,OA=OB,AP=AC,
∴∠OAP=∠BAC,
∴△OAP≌△BAC,
∴∠AOP=∠CBA=90°,
在Rt△ABM中,∵∠ABM=90°,AB=OA=4,∠BAM=60°,
∴AM=2AB=8,
∴OM=AM-OA=4,
∴M(4,0).
(3) 结论:OP=CD+![]() AD.
AD.
理由:如图3中,取AD的中点R,连接BR、OR.
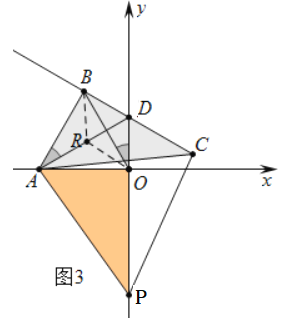
∵∠ABD=∠AOD=90°,AR=DR,
∴BR=AR=RD=OR,
∴A、B、E、O四点共圆,
∴∠BAD=∠BOD=90°-60°=30°,
∴BD=![]() AD,
AD,
∵△ABO,△APC都是等边三角形,
∴∠OAB=∠PAC,OA=OB,AP=AC,
∴∠OAP=∠BAC,
∴△OAP≌△BAC,
∴OP=BC=CD+BD=CD+![]() AD.
AD.
即OP=CD+![]() AD.
AD.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.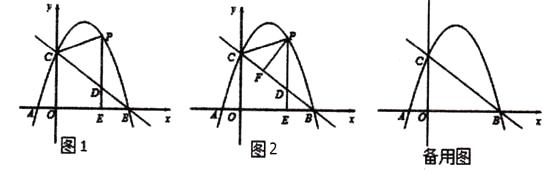
(1)试求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
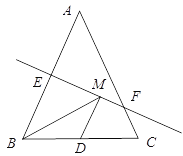
【题目】如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;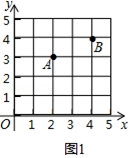
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.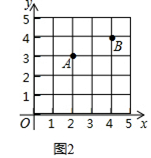
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织学生乘汽车去自然保护区野营,先以60km/h的速度走平路,后又以30km/h的速度爬坡,共用了6.5h;原路返回时,汽车以40km/h的速度下坡,又以50km/h的速度走平路,共用了6 h。问平路和坡路各有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )

A. 105° B. 110° C. 100° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知DE∥BC, AB∥CD,E为AB的中点,∠A=∠B.下列结论:①CD=AE;②AC=DE;③AC平分∠BCD;④O点是DE的中点;⑤AC=AB.其中正确的是( )
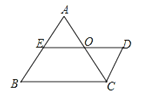
A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论正确的有__________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com