
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.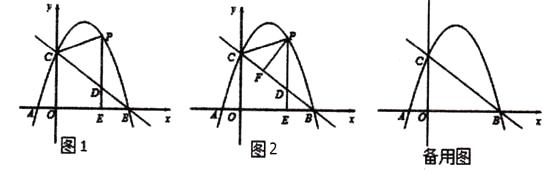
(1)试求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.
【答案】
(1)
解:由OC=3OA, 有:C(0,3),
将 A(-1,0)、B(4,0),C(0,3)代入y=ax2+bx+c中,
得 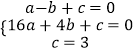 解之得:
解之得: 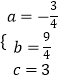 ,
,
故y= ![]() 即为所求.
即为所求.
(2)
解:设P(m, ![]() ),△PFD的周长为L,
),△PFD的周长为L,
∵直线BC经过B(4,0),C(0,3),易得直线BC的解析式为:yBC= ![]() ,
,
则D(m, ![]() ),PD=
),PD= ![]() ,
,
∵PE⊥x轴,PE//OC,
∴∠BDE=∠BCO,
又∠BDE=∠PDF,
∴∠PDF=∠BCO,
而∠PFD=∠BOC=90°,
∴△PFD~△BOC.
![]() ,
,
由(1)知,OC=3,OB=4,则BC=5,
故△BOC的周长为12,
∴ ![]() 即:L=
即:L= ![]() (m-2)2+
(m-2)2+ ![]() ,
,
∴当m=2时,L最大= ![]() .
.
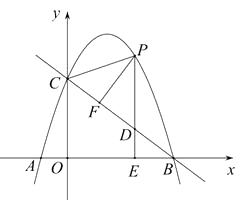
(3)
解:存在这样的Q点,使得四边形CDPQ是菱形.
当点Q落在y轴上时,四边形CDPQ是菱形,
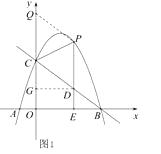
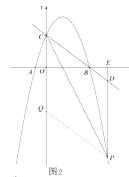
∵由轴对称的性质知,CD=CQ,PQ=PD,∠PCQ=∠PCD,
当点Q落在y 轴上时,CQ∥PD,∴∠PCQ=∠CPD,
∴∠PCD=∠CPD,
∴CD=PD,
∴CD=DP=PQ=QC,
∴四边形CDPQ是菱形,
如图1,过点D作DG⊥y轴于点G,
设P(n, ![]() ),则D(n,
),则D(n, ![]() ),G(0,
),G(0, ![]() ),
),
在Rt△CGD中,CD2=CG2+GD2= ![]() =
= ![]() ,
,
而PD= ![]() ,
,
∵ PD=CD,
∴ ![]() ①
①
或 ![]() ②
②
解方程①得:n= ![]() 或n=0(不符合题意,舍去),
或n=0(不符合题意,舍去),
解方程②得:n= ![]() 或n=0(不符合题意,舍去).
或n=0(不符合题意,舍去).
当n= ![]() 时,P(
时,P( ![]() ,
, ![]() ),
),
当n= ![]() 时,P(
时,P( ![]() ,
, ![]() ).
).
综上所述,存在这样的P点,使得四边形CDPQ为菱形,此时点P的坐标为P( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)由OC=3OA,求出点C坐标,再运用待定系数法求;(2)易证得△PFD~△BOC,由相似三角形的周长比等于相似比,求出△PFD的周长与点P横坐标的关系,再求最值;(3)由PD//y轴,且CP为四边形CDPQ的对角线,则Q在y轴上时,四边形CDPQ为菱形,根据PD=CD,列方程解出答案.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
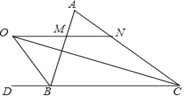
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
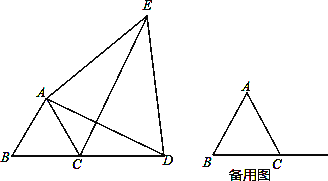
【题目】如图,已知△ABC为等边三角形,点D由点C出发,在BC的延长线上运动,连结AD,以AD为边作等边三角形ADE,连结CE.
(1)请写出AC、CD、CE之间的数量关系,并证明;
(2)若AB=6cm,点D的运动速度为每秒2cm,运动时间为t秒,则t为何值时,CE⊥AD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表所 示是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/ 吨 | 单价:元/ 吨 |
17 吨以下 | a | 0.80 |
超过 17 吨但不超过 30 吨的部分 | b | 0.80 |
超过 30 吨的部分 | 6.00 | 0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费自来水费用 污水处理费用)
已知小明家 2017 年 5 月份用水 20 吨,交水费 66 元;6 月份用水 25 吨交水费91元;
(1)求a 、b 的值;
(2)为了节约开支,小明家计划把 7 月份的水费控制在不超过家庭月收入的2% .若小明家的月收入为 9200 元,则小明家 7 月份最多能用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边△OAB的顶点A在x轴的负半轴上,点B(a,b)在第二象限内,且a,b满足![]() .点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
.点P是y轴上的一个动点,以PA为边作等边△PAC,直线BC交x轴于点M,交y轴于点D.
(1)求点A的坐标;
(2)如图2,当点P在y轴正半轴上时,求点M的坐标;
(3)如图3,当点P在y轴负半轴上时,求出OP,CD,AD满足的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com