
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
【答案】A
【解析】解:在同一坐标系xOy中,画出函数二次函数y=﹣x2+1与正比例函数y=﹣x的图象,如图所示.设它们交于点A、B. 令﹣x2+1=﹣x,即x2﹣x﹣1=0,解得:x= ![]() 或
或 ![]() ,
,
∴A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ).
).
观察图象可知:
① 当x≤ ![]() 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为
时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而增大,其最大值为 ![]() ;
;
②当 ![]() <x<
<x< ![]() 时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为
时,min{﹣x2+1,﹣x}=﹣x,函数值随x的增大而减小,其最大值为 ![]() ;
;
③当x≥ ![]() 时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为
时,min{﹣x2+1,﹣x}=﹣x2+1,函数值随x的增大而减小,最大值为 ![]() .
.
综上所示,min{﹣x2+1,﹣x}的最大值是 ![]() .
.
故选:A.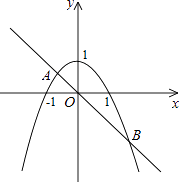
理解min{a,b}的含义就是取二者中的较小值,画出函数图象草图,利用函数图象的性质可得结论.


科目:初中数学 来源: 题型:
【题目】现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂在A、B两种不同规格的货车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元.
(1)设运送这批货物的总费用为y万元,这列货车挂A型车厢x 节,试定出用车厢节数x表示总费用y的公式.
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+3的图象与x轴,y轴交于A,B两点,与反比例函数 ![]() 的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
的图象相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE.有下列四个结论:
①△CEF与△DEF的面积相等;
②△AOB∽△FOE;
③△DCE≌△CDF;
④AC=BD.
其中正确的结论是( )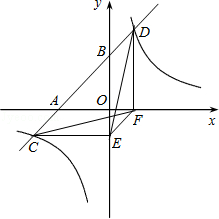
A.①②
B.①②③
C.①②③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学、外语、语文及其他学科中,某校七年级开展了“同学们最喜欢哪门学科”的调查(该校七年级共有200人,每人只能选一项).
(1)调查的问题是什么?调查的对象是谁?
(2)在被调查的200名学生中,有40人最喜欢语文,60人最喜欢数学,80人最喜欢外语,其余的人选择其他.请把七年级的学生最喜欢某学科的人数及其占学生总数的百分比填入下表:
语文 | 外语 | 数学 | 其他 | |
人数 | ||||
占学生总数的百分比 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且BC=8cm,CA=6cm,则点O到边AB的距离为( )
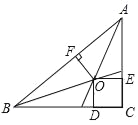
A. 2cm B. 3cm C. 4cm D. 5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.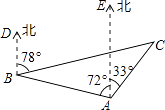
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点F在线段DE上,且EF=2DF,过点C的直线CG交OA的延长线于点G,且∠CGO=∠CDE. 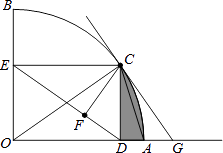
(1)求证:CG与弧AB所在圆相切.
(2)当点C在弧AB上运动时,△CFD的三条边是否存在长度不变的线段?若存在,求出该线段的长度;若不存在,说明理由.
(3)若∠CGD=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3经过A(-1,0)、B(3,0)两点,与y轴交于C点,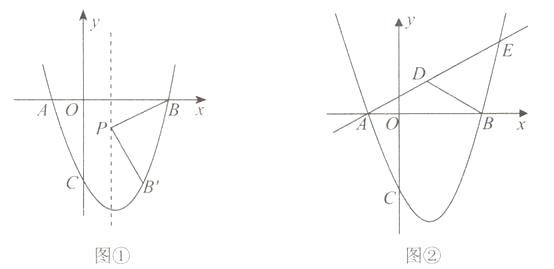
(1)求抛物线的解析式;
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标;
(3)如图②,直线y= ![]() x+
x+ ![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.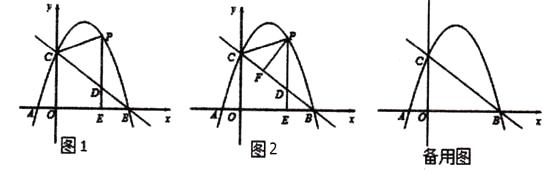
(1)试求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com