
【题目】已知抛物线y=ax2+bx-3经过A(-1,0)、B(3,0)两点,与y轴交于C点,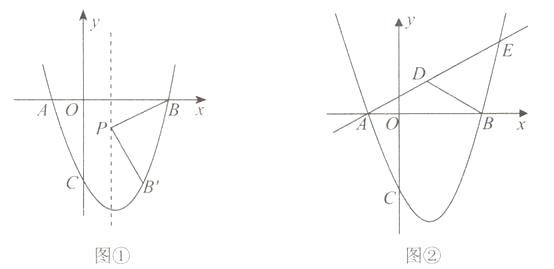
(1)求抛物线的解析式;
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标;
(3)如图②,直线y= ![]() x+
x+ ![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】
(1)
解:将A(-1,0)、B(3,0)代入抛物线y=ax2+bx-3可得
![]() ,解得
,解得 ![]()
∴抛物线的解析式为:y=x2-2x-3.
(2)
解:作B′M⊥对称轴,垂足为M,
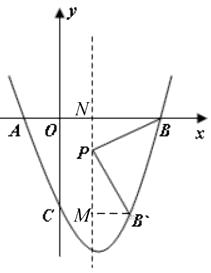
∵∠BPB′=90°,
∴∠BPN+∠B′PM=90°,
∵∠BPN+∠PBN=90°,
∴∠PBN=∠B′PM,
∵∠BNP=∠PMB′=90°,PB=PB′,
∴△BNP≌△PMB′,
∴BN=PM,PN=MB′,
由A(-1,0)、B(3,0)得对称轴为 x=1,
∴BN=3-1=2,
设P(1,m),∴B′(1-m,m-2),
将B′(1-m,m-2)代入y=x2-2x-3,得(1-m)2-2(1-m)-3=m-2,
解得m1=-1,m2=2,
∵点P在x轴下方,∴m=-1,
∴P(1,-1).
(3)
解:存在.∵直线y= ![]() 与y轴的交点为:G(0,
与y轴的交点为:G(0, ![]() ),
),
与x轴的交点为:A(-1,0),
∴tan∠GAO= ![]() ,∴∠GAO=30°,
,∴∠GAO=30°,
过点E作EF∥x轴,过点D作DF⊥EF,垂足为F,
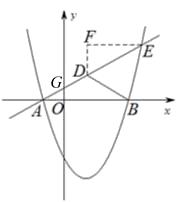
∴∠FED=∠GAO=30°,∴DE=2DF,DF= ![]() ,
,
设点Q的运动时间为t秒,则:t= ![]() ,
,
∴当BD⊥x轴时,此时,B、D、F在同一直线上,且BF⊥EF,
根据垂线段最短可得:此时BD+DF最小,
此时点Q的运动时间t秒最少,如下图:
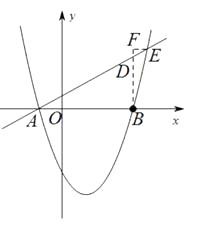
将x=3代入y= ![]() 得y=
得y= ![]() ,
,
∴D(3, ![]() ).
).
【解析】(1)将A(-1,0),B(3,0)代入抛物线解析式,列得方程组解出a,b即可;(2)作B′M⊥对称轴,垂足为M,证明△BNP≌△PMB′,可设P(1,m),用m表示出点B′的坐标,将其代入抛物线解析式,即可求得m;(3)由题可知要求“t= ![]() ”的最小值;过点E作EF∥x轴,过点D作DF⊥EF,垂足为F,由直线y=
”的最小值;过点E作EF∥x轴,过点D作DF⊥EF,垂足为F,由直线y= ![]() 易证得∠FED=∠GAO=30°,则可得DF=
易证得∠FED=∠GAO=30°,则可得DF= ![]() ,即
,即 ![]() ,则当B,D,F三点一线时,BD+DF最小.
,则当B,D,F三点一线时,BD+DF最小.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
【题目】1或5 △ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为

A. 2 B. 3 C. 2或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC延长线于F,则下列结论:①△APE△DQE;②PQ=EF;③当P为AB中点时,CF= ![]() ;④若H为QC中点,当P从A移动到B时,线段EH扫过的面积为
;④若H为QC中点,当P从A移动到B时,线段EH扫过的面积为 ![]() .其中正确的是( )
.其中正确的是( )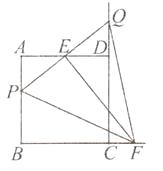
A.①②
B.①②④
C.②③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为a,将此正方形按照下面的方法进行剪拼:第一次,先沿正方形的对边中点连线剪开,然后对接为一个长方形,则此长方形的周长为___;第二次,再沿长方形的对边(长方形的宽)中点连线剪开,对接为新的长方形,如此继续下去,第n次得到的长方形的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(0,6)的直线AB与直线OC相交于点C(2,4)动点P沿路线O→C→B运动.(1)求直线AB的解析式;(2)当△OPB的面积是△OBC的面积的![]() 时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.
时,求出这时点P的坐标;(3)是否存在点P,使△OBP是直角三角形?若存在,直接写出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.
运用上述知识,解决下列问题:
(1)如果(a-2)![]() +b+3=0,其中a、b为有理数,那么a= ,b= ;
+b+3=0,其中a、b为有理数,那么a= ,b= ;
(2)如果(2+![]() )a-(1-
)a-(1-![]() )b=5,其中a、b为有理数,求a+2b的值.
)b=5,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
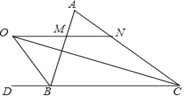
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表所 示是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/ 吨 | 单价:元/ 吨 |
17 吨以下 | a | 0.80 |
超过 17 吨但不超过 30 吨的部分 | b | 0.80 |
超过 30 吨的部分 | 6.00 | 0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费自来水费用 污水处理费用)
已知小明家 2017 年 5 月份用水 20 吨,交水费 66 元;6 月份用水 25 吨交水费91元;
(1)求a 、b 的值;
(2)为了节约开支,小明家计划把 7 月份的水费控制在不超过家庭月收入的2% .若小明家的月收入为 9200 元,则小明家 7 月份最多能用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com