
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表所 示是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/ 吨 | 单价:元/ 吨 |
17 吨以下 | a | 0.80 |
超过 17 吨但不超过 30 吨的部分 | b | 0.80 |
超过 30 吨的部分 | 6.00 | 0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费自来水费用 污水处理费用)
已知小明家 2017 年 5 月份用水 20 吨,交水费 66 元;6 月份用水 25 吨交水费91元;
(1)求a 、b 的值;
(2)为了节约开支,小明家计划把 7 月份的水费控制在不超过家庭月收入的2% .若小明家的月收入为 9200 元,则小明家 7 月份最多能用水多少吨?
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3经过A(-1,0)、B(3,0)两点,与y轴交于C点,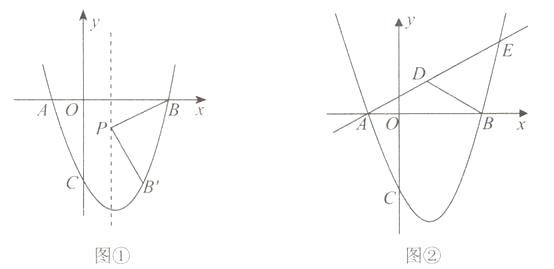
(1)求抛物线的解析式;
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标;
(3)如图②,直线y= ![]() x+
x+ ![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒钟2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少,若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.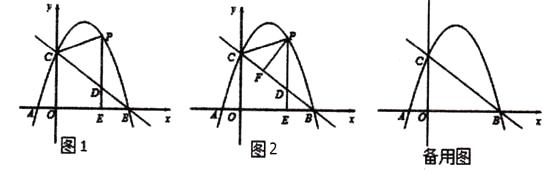
(1)试求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知直线
中,已知直线 ![]() (
( ![]() )分别交反比例函数
)分别交反比例函数 ![]() 和
和 ![]() 在第一象限的图象于点
在第一象限的图象于点 ![]() ,
, ![]() ,过点
,过点 ![]() 作
作 ![]() 轴于点
轴于点 ![]() ,交
,交 ![]() 的图象于点
的图象于点 ![]() ,连结
,连结 ![]() .若
.若 ![]() 是等腰三角形,则
是等腰三角形,则 ![]() 的值是 .
的值是 . 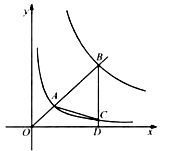
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
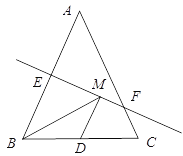
【题目】如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点A(2,3),B(4,4),请在所给网格区域(含边界)上按要求画整点三角形.
(1)在图1中画一个△PAB,使点P的横、纵坐标之和等于点A的横坐标;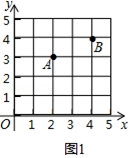
(2)在图2中画一个△PAB,使点P,B横坐标的平方和等于它们纵坐标和的4倍.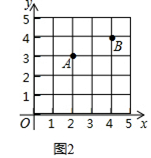
查看答案和解析>>
科目:初中数学 来源: 题型:
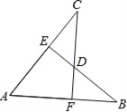
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论正确的有__________.(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com