
【题目】如图, ![]() 为
为 ![]() 的直角边
的直角边 ![]() 上一点,以
上一点,以 ![]() 为半径的
为半径的 ![]() 与斜边
与斜边 ![]() 相切于点
相切于点 ![]() ,交
,交 ![]() 于点
于点 ![]() .已知
.已知 ![]() ,
, ![]() .
.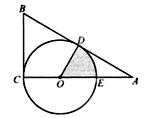
(1)求 ![]() 的长;
的长;
(2)求图中阴影部分的面积.
【答案】
(1)
解:在Rt△ABC中,AB=![]() =
=![]() =2
=2 ![]() .
.
∵BC⊥OC
∴BC是⊙O的切线
又∵AB是⊙O的切线
∴BD=BC=![]()
∴AD=AB-BD=![]()
(2)
解:在Rt△ABC中,sinA= ![]() =
=![]() =
=![]() .
.
∴∠A=30°.
∵AB切⊙O于点D.
∴OD⊥AB.
∴∠AOD=90°-∠A=60°.
∵ ![]() =tanA=tan30°.
=tanA=tan30°.
∴ ![]() =
=![]() .
.
∴OD=1.
S阴影=![]() =
=![]() .
.
【解析】(1)在Rt△ABC中,利用勾股定理求出AB的长,然后根据切线的判定证出BC为切线,然后可根据切线长定理可求解.
(2)在Rt△ABC中,根据∠A的正弦求出∠A度数,然后根据切线的性质求出OD的长,和扇形圆心角的度数,再根据扇形的面积公式可求解.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为a,将此正方形按照下面的方法进行剪拼:第一次,先沿正方形的对边中点连线剪开,然后对接为一个长方形,则此长方形的周长为___;第二次,再沿长方形的对边(长方形的宽)中点连线剪开,对接为新的长方形,如此继续下去,第n次得到的长方形的周长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
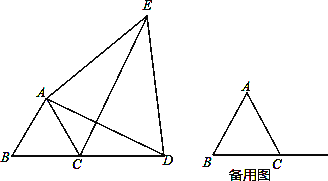
【题目】如图,已知△ABC为等边三角形,点D由点C出发,在BC的延长线上运动,连结AD,以AD为边作等边三角形ADE,连结CE.
(1)请写出AC、CD、CE之间的数量关系,并证明;
(2)若AB=6cm,点D的运动速度为每秒2cm,运动时间为t秒,则t为何值时,CE⊥AD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.如表所 示是该市居民“一户一表”生活用水及提示计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/ 吨 | 单价:元/ 吨 |
17 吨以下 | a | 0.80 |
超过 17 吨但不超过 30 吨的部分 | b | 0.80 |
超过 30 吨的部分 | 6.00 | 0.80 |
(说明:①每户产生的污水量等于该户自来水用水量;②水费自来水费用 污水处理费用)
已知小明家 2017 年 5 月份用水 20 吨,交水费 66 元;6 月份用水 25 吨交水费91元;
(1)求a 、b 的值;
(2)为了节约开支,小明家计划把 7 月份的水费控制在不超过家庭月收入的2% .若小明家的月收入为 9200 元,则小明家 7 月份最多能用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中, 放置一副三角板 ABO(OAB 90 ,OBA AOB 45 ,OA AB) , BO 边与 x 轴重合,其中一个45角的顶点在原点O ,直角顶点 A 在第一象限内.
(1)将另一个三角板 DEF 如图 1 放置, EDF 90 ,直角顶点 D 置于 AO 边上(不与O 重合),此时, DE 交 y 轴于 M 点, DF 交 x 轴于 N 点,求证:DM DN .
(2)如图 2, D 是线段 AB 上一动点,连接OD ,过O 作OE OD ,取点 E 满足OE OD .连接 EB 交OA 于点 P ,探究![]() 的值是否为定值,若是定值,求出其值;若不是定值,说明理由.
的值是否为定值,若是定值,求出其值;若不是定值,说明理由.
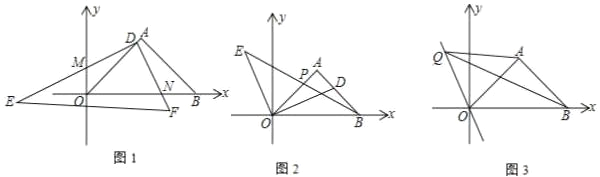
(3)如图 3,直线a 经过原点且与 y 轴成22.5角,Q 是 x 轴上方直线a 上一动点,连接 AQ 、 BQ ,请比较OB OA 与QA QB 的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D,且AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )

A. 80° B. 70° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( ) 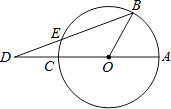
A.DE=EB
B.![]() DE=EB
DE=EB
C.![]() DE=DO
DE=DO
D.DE=OB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com