
【题目】在直角坐标系中, 放置一副三角板 ABO(OAB 90 ,OBA AOB 45 ,OA AB) , BO 边与 x 轴重合,其中一个45角的顶点在原点O ,直角顶点 A 在第一象限内.
(1)将另一个三角板 DEF 如图 1 放置, EDF 90 ,直角顶点 D 置于 AO 边上(不与O 重合),此时, DE 交 y 轴于 M 点, DF 交 x 轴于 N 点,求证:DM DN .
(2)如图 2, D 是线段 AB 上一动点,连接OD ,过O 作OE OD ,取点 E 满足OE OD .连接 EB 交OA 于点 P ,探究![]() 的值是否为定值,若是定值,求出其值;若不是定值,说明理由.
的值是否为定值,若是定值,求出其值;若不是定值,说明理由.
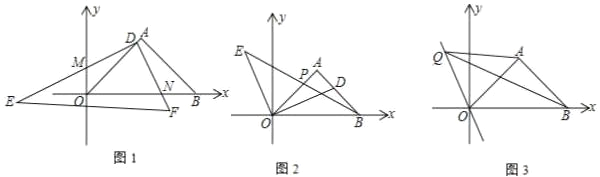
(3)如图 3,直线a 经过原点且与 y 轴成22.5角,Q 是 x 轴上方直线a 上一动点,连接 AQ 、 BQ ,请比较OB OA 与QA QB 的大小关系,并说明理由.
【答案】(1)详见解析.(2)![]() 的值是定值,其值为
的值是定值,其值为![]() ,理由详见解析;(3)AQ BQ OA OB ,理由详见解析.
,理由详见解析;(3)AQ BQ OA OB ,理由详见解析.
【解析】
(1)先判断出∠IDM=∠KDN,得出DI=DK,进而得出△DIM≌△DKN,即可得出结论;
(2)先表示出点A,B坐标,进而得出直线OA,AB的解析式,即可得出ON,DN,BD,再判断出△OME≌△DNO,得出OM=DN=-n+2m,EM=ON=n,进而得出直线BE解析式,即可求出点A坐标,进而得出AP,即可得出结论;
(3)先判断出OQ是AA'的垂直平分线,进而得出A'Q=AQ,最后用三角形的三边关系即可得出结论.
(1)如图1,
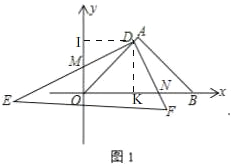
过点D作DI⊥y轴于I,DK⊥x轴于K,
∴四边形OIDK是矩形,
∴∠IDK=90,
∵∠EDF=90,
∴∠IDM=∠KDN
∵△AOB是等腰直角三角形,
∴直线OA的解析式为y=x,
∴DI=DK,
在△DIM和△DKN中,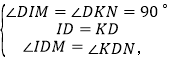
∴△DIM≌△DKN,
∴DM=DN;
(2)![]() 的值是定值,其值为:
的值是定值,其值为:![]() ,
,
理由:如图2,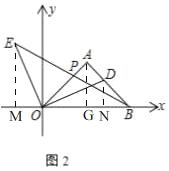
过点A作AG⊥OB于G,
∵△AOB是等腰直角三角形,
∴OG=BG=AG,
设OG=BG=AG=m,
∴OB=2m,
∴A(m,m),B(2m,0),
∴直线OA的解析式为y=x①,直线OB的解析式为y=x+2m,
设D(n,n+2m)![]()
过点D作DN⊥OB于N,
∴ON=n,DN=n+2m,
∴![]()
过点E作EM⊥OB于M,
∴∠OME=90=∠DNO,
∴∠OEM+∠EOM=90,
∵OD⊥OE,
∴∠DOE=90,
∴∠EOM+∠DON=90,
∴∠OEM=∠DON,
∵OM=OD,
∴△OME≌△DNO,
∴OM=DN=n+2m,EM=ON=n,
∴E(n2m,n),
∵B(2m,0),
∴直线BE的解析式为![]() ②/span>,
②/span>,
联立①②解得,![]()
∴![]()
∵A(m,m),
∴![]()
∴![]()
(3)AQ+BQ>OA+OB,理由:如图3,
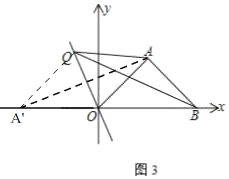
在x轴的负半轴上取一点A′,使OA′=OA,连接QA′,AA′,
∵直线a经过原点且与y轴成22.5角,
∴∠AOQ=45+22.5=67.5,
∴∠A′OQ′=180∠AOQ∠AOB=67.5=∠AOQ,
∴OQ⊥AA′,
∴AQ是AA′的垂直平分线,
∴AQ=A′Q,在△A′BQ中,A′Q+BQ>A′B,
∵A′B=OA′+OB=OA+OB,
∴AQ+BQ>OA+OB.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
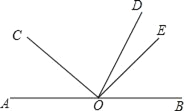
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
查看答案和解析>>
科目:初中数学 来源: 题型:
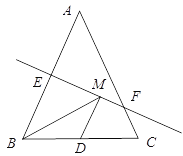
【题目】如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
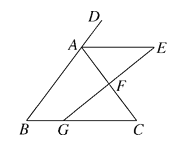
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织学生乘汽车去自然保护区野营,先以60km/h的速度走平路,后又以30km/h的速度爬坡,共用了6.5h;原路返回时,汽车以40km/h的速度下坡,又以50km/h的速度走平路,共用了6 h。问平路和坡路各有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:已知:10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com