练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知DE∥BC， AB∥CD，E为AB的中点，∠A=∠B．下列结论：①CD=AE；②AC=DE；③AC平分∠BCD；④O点是DE的中点；⑤AC=AB．其中正确的是（　　）

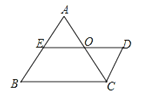
    A. ①②④ B. ①③⑤ C. ②③④ D. ②④⑤

    【答案】A

    【解析】试题分析：∵已知DE∥BC，AB∥CD，∴四边形BCDE为平行四边形，∴CB=DE；

    ∵∠A=∠B，∴AC=BC， ∴AC=DE，即可得②正确；

    根据平行线等分线段性质可得AO=CO，∵AB∥CD，∴∠A=∠DCO，

    又∵∠AOE=∠COD， ∴△AOE≌△COD（ASA）， ∴AE=CD，即可得①正确；

    OE=OD，O点是DE的中点；即可得④正确；结论③⑤无法证明．故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

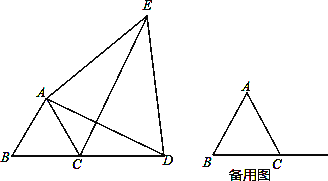
    【题目】如图，已知△ABC为等边三角形，点D由点C出发，在BC的延长线上运动，连结AD，以AD为边作等边三角形ADE，连结CE．

    （1）请写出AC、CD、CE之间的数量关系，并证明；

    （2）若AB=6cm，点D的运动速度为每秒2cm，运动时间为t秒，则t为何值时，CE⊥AD？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等腰△ABC中，AB＝AC，∠A＝20°，AB上一点D，且AD＝BC，过点D作DE∥BC且DE＝AB，连接EC，则∠DCE的度数为（ ）

    A. 80° B. 70° C. 60° D. 45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，等边△OAB的顶点A在x轴的负半轴上，点B（a，b）在第二象限内，且a，b满足.点P是y轴上的一个动点，以PA为边作等边△PAC，直线BC交x轴于点M，交y轴于点D.

    (1)求点A的坐标；

    (2)如图2，当点P在y轴正半轴上时，求点M的坐标；

    (3)如图3，当点P在y轴负半轴上时，求出OP，CD，AD满足的数量关系，并证明你的结论.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】仔细阅读下面的例题：

    例题：已知二次三项式x2－4x＋m有一个因式是x＋3，求另一个因式以及m的值．

    解：设另一个因式为x＋n，则

    x2－4x＋m＝(x＋3)(x＋n)，

    ∴x2－4x＋m＝x2＋(n＋3)x＋3n，

    ∴，解得，

    ∴另一个因式为x－7，m的值为－21.

    问题：仿照以上方法解答下面的问题：

    已知二次三项式2x2＋3x－k有一个因式是2x－5，求另一个因式以及k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法中，正确的是( )

    A. 平面内，没有公共点的两条线段平行

    B. 平面内，没有公共点的两条射线平行

    C. 没有公共点的两条直线互相平行

    D. 互相平行的两条直线没有公共点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AC是⊙O的直径，点B在圆周上（不与A、C重合），点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（ ）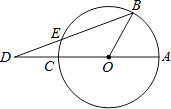
    A.DE=EB
    B. DE=EB
    C. DE=DO
    D.DE=OB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校改造一个边长为米的正方形花坛，经规划后，南北向要缩短米，东西向要加长米，则改造后花坛的面积是________平方米，改造后花坛的面积减少了________平方米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点，在日常生活中，人们更倾向于LED灯的使用，某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况，进行了市场调查：某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售，其进价与标价如下表：

    LED灯泡

    普通白炽灯泡

    进价（元）

    45

    25

    标价（元）

    60

    30


    （1）该商场购进了LED灯泡与普通白炽灯泡共300个，LED灯泡按标价进行销售，而普通白炽灯泡打九折销售，当销售完这批灯泡后可以获利3200元，求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个？
    （2）由于春节期间热销，很快将两种灯泡销售完，若该商场计划再次购进两种灯泡120个，在不打折的情况下，请问如何进货，销售完这批灯泡时获利最多且不超过进货价的30%，并求出此时这批灯泡的总利润为多少元？

    查看答案和解析>>

    同步练习册答案