
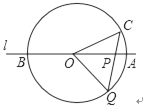
【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
【答案】40°、20°、100°.
【解析】
点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
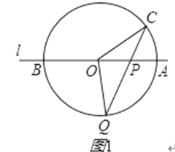
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°﹣∠QOC)×![]() ①,
①,
∵OQ=PQ,
∴∠OPQ=(180°﹣∠OQP)×![]() ②,
②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
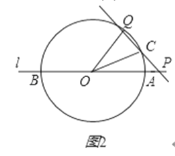
③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°﹣∠COQ)×![]() ①,
①,
∵OQ=PQ,
∴∠P=(180°﹣∠OQP)×![]() ②,
②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°﹣150°﹣10°=20°.
故答案为:40°、20°、100°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
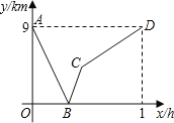
【题目】小明骑电动车从甲地去乙地,而小刚骑自行车从乙地去甲地,两人同时出发走相同的路线;设小刚行驶的时间为x(h),两人之间的距离为y(km),图中的折线表示y与x之间的函数关系,点B的坐标为(![]() ,0).根据图象进行探究:
,0).根据图象进行探究:
(1)两地之间的距离为______km;
(2)请解释图中点B的实际意义;
(3)求两人的速度分别是每小时多少km?
(4)直接写出点C的坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
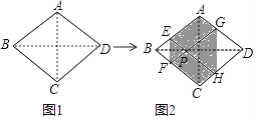
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;②当x= ![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
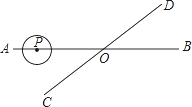
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么________秒种后⊙P与直线CD相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=30°,点P是∠AOB 内部及射线OB上一点,且OP=10cm.
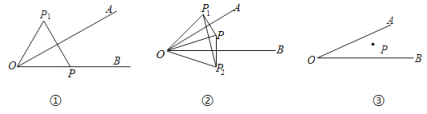
(1)若点P在射线OB上,过点P作关于直线OA的对称点![]() ,连接O
,连接O![]() 、P
、P![]() , 如图①求P
, 如图①求P![]() 的长.
的长.
(2)若过点P分别作关于直线OA、直线OB的对称点![]() 、
、![]() ,连接O
,连接O![]() 、O
、O![]() 、
、![]()
![]() 如图②, 求
如图②, 求![]()
![]() 的长.
的长.
(3)若点P在∠AOB 内,分别在射线OA、射线OB找一点M,N,使△PMN的周长取最小值,请直接写出这个最小值.如图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
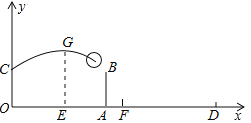
【题目】如图,已知排球场的长度OD为18 m,位于球场中线处球网的高度AB为2.4 m,一队员站在点O处发球,排球从点O的正上方1.6 m的C点向正前方飞出,当排球运行至离点O的水平距离OE为6 m时,到达最高点G建立如图所示的平面直角坐标系
(1) 当球上升的最大高度为3.4 m时,对方距离球网0.4 m的点F处有一队员,他起跳后的最大高度为3.1 m,问这次她是否可以拦网成功?请通过计算说明
(2) 若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com