
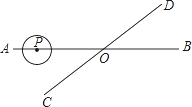
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么________秒种后⊙P与直线CD相切.
【答案】4或8
【解析】
分类讨论:当点P在当点P在射线OA时⊙P与CD相切,过P作PE⊥CD与E,根据切线的性质得到PE=1cm,再利用含30°的直角三角形三边的关系得到OP=2PE=2cm,则⊙P的圆心在直线AB上向右移动了(6-2)cm后与CD相切,即可得到⊙P移动所用的时间;当点P在射线OB时⊙P与CD相切,过P作PE⊥CD与F,同前面一样易得到此时⊙P移动所用的时间.
解:当点P在射线OA时⊙P与CD相切,如图,过P作PE⊥CD与E,
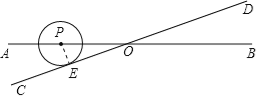
∴PE=1cm,
∵∠AOC=30°,
∴OP=2PE=2cm,
∴⊙P的圆心在直线AB上向右移动了(6-2)cm后与CD相切,
∴⊙P移动所用的时间=![]() =4(秒);
=4(秒);
当点P在射线OB时⊙P与CD相切,如图,过P作PE⊥CD与F,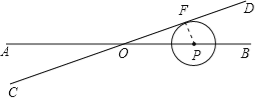
∴PF=1cm,
∵∠AOC=∠DOB=30°,
∴OP=2PF=2cm,
∴⊙P的圆心在直线AB上向右移动了(6+2)cm后与CD相切,
∴⊙P移动所用的时间=![]() =8(秒).
=8(秒).
故答案为4或8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票原定的票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠措施,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°. 求小岛B到河边公路AD的距离.
(参考数据:sin37°≈ 0.60,cos37° ≈ 0.80,tan37° ≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
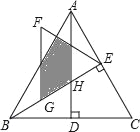
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
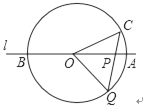
【题目】如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天课间,顽皮的小明同学拿着老师的等腰三角板玩,不小心掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.
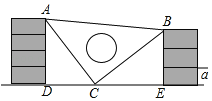
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10cm,请你帮小明求出三角板ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com