
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() , 垂足为
, 垂足为![]() ,
,![]() ,
,![]() 和
和![]() 的面积分别为50和37, 则
的面积分别为50和37, 则![]() 的面积为__________.
的面积为__________.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
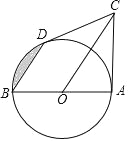
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
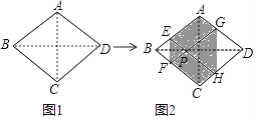
【题目】如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是菱形ABCD的中心;②当x= ![]() 时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是
时,EF+GH>AC;③当0<x<2时,六边形AEFCHG面积的最大值是 ![]() ;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
;④当0<x<2时,六边形AEFCHG周长的值不变.其中正确结论是________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。

(1)如图1,直接写出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
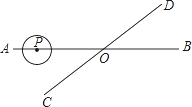
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么________秒种后⊙P与直线CD相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com