
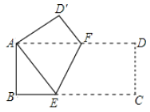
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,将矩形沿
,将矩形沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,则折痕
重合,则折痕![]() 的长为( )
的长为( )
A.6B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据折叠的性质得到EF垂直平分AC,即OA=OC,FA=FC,∠AOF=90°,设AF=x,则FC=x,BF=BC-x=10-x,在Rt△ABF中根据勾股定理列方程可计算出x,在Rt△ABC中根据勾股定理可计算出AC,可得OA的长,在Rt△AOF中利用勾股定理可计算出OF;易证得△AOE≌△COF,得到OE=OF,则EF=2OF.
解:连结AC,如图,
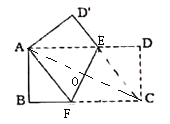
∵矩形折叠后点C与点A重合,
∴EF垂直平分AC,即OA=OC,FA=FC,∠AOF=90°,
设AF=x,则FC=x,BF=BC-x=10-x,
在Rt△ABF中,AB2+BF2=AF2,即52+(10-x)2=x2,解得x=![]() ,
,
在Rt△ABC中,AC=![]() =
=![]() ,
,
∴OA=![]() ,
,
在Rt△AOF中,OF=![]() =
=![]() ,
,
∵AD∥BC,
∴∠DAC=∠BCA,
∵在△AOE和△COF中, ,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∴EF=2OF=![]() .
.
故选:D.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
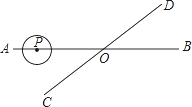
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么________秒种后⊙P与直线CD相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
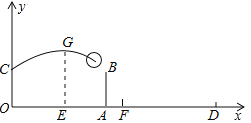
【题目】如图,已知排球场的长度OD为18 m,位于球场中线处球网的高度AB为2.4 m,一队员站在点O处发球,排球从点O的正上方1.6 m的C点向正前方飞出,当排球运行至离点O的水平距离OE为6 m时,到达最高点G建立如图所示的平面直角坐标系
(1) 当球上升的最大高度为3.4 m时,对方距离球网0.4 m的点F处有一队员,他起跳后的最大高度为3.1 m,问这次她是否可以拦网成功?请通过计算说明
(2) 若队员发球既要过球网,又不出边界,问排球飞行的最大高度h的取值范围是多少?(排球压线属于没出界)
查看答案和解析>>
科目:初中数学 来源: 题型:
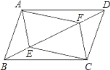
【题目】在四边形![]() 中,点
中,点![]() 、
、![]() 是对角线
是对角线![]() 上的两点,且
上的两点,且![]() .则下列结论中,错误的是( )
.则下列结论中,错误的是( )
A. 若四边形![]() 是平行四边形,则
是平行四边形,则![]() 也是平行四边形
也是平行四边形
B. 若四边形![]() 是菱形,则四边形
是菱形,则四边形![]() 也是菱形
也是菱形
C. 若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 也是矩形
也是矩形
D. 若四边形![]() 是正方形,则四边形
是正方形,则四边形![]() 一定是菱形
一定是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,且AD=12cm.点P从点A出发,以3cm/s的速度在射线AD上运动;同时,点Q从点C出发,以1cm/s的速度在射线CB上运动.运动时间为t,当t=______秒(s)时,点P、Q、C、D构成平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E且AB=AE,延长AB与DE的延长线相交于点F,连接AC、CF.下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③BF=AD;④S△BEF=S△ABC;⑤S△CEF=S△ABE;其中正确的有( )

A.2个B.3个C.4个D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com