
【题目】某个体小服装店主准备在夏季来临前,购进甲、乙两种T恤.两种T恤的相关信息如表:
品牌 | 甲 | 乙 |
进价(元/件) | 45 | 80 |
售价(元/件) | 75 | 120 |
根据上述信息,该店决定用不少于6198元,但不超过6296元的资金购进这两种T恤共100件请解答下列问题:
(1)该店有哪几种进货方案?
(2)该店按哪种方案进货所获利润最大,最大利润是多少?
【答案】(1)有三种进货方案,方案一:购进甲种T恤49件,乙种T恤51件;方案二:购进甲种T恤50件,乙种T恤50件;方案三:购进甲种T恤51件,乙种T恤49件;(2)方案一该店购进甲种T恤49件,乙种T恤51件时获利最大,最大利润为3510元.
【解析】
(1)设购进甲种T恤x件,则购进乙种T恤(100﹣x)件,根据总价=单价×数量结合总价不少于6198元且不超过6296元,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,再结合x为整数即可得出各进货方案;
(2)设所获得利润为W元,根据总利润=每件的利润×销售数量(购进数量),即可得出W关于x的函数关系式,再利用一次函数的性质即可解决最值问题.
解:(1)设购进甲种T恤x件,则购进乙种T恤(100﹣x)件.
依题意,得:![]() ,
,
解得:48![]() ≤x≤51
≤x≤51![]() .
.
∵x为正整数,
∴x=49,50,51.
∴有三种进货方案,方案一:购进甲种T恤49件,乙种T恤51件;方案二:购进甲种T恤50件,乙种T恤50件;方案三:购进甲种T恤51件,乙种T恤49件.
(2)设所获得利润为W元.
依题意,得:W=(75﹣45)x+(120﹣80)(100﹣x)=﹣10x+4000.
∵k=﹣10<0,
∴W值随x值的增大而减小,
∴当x=49时,W取得最大值,最大值=﹣10×49+4000=3510.
答:方案一该店购进甲种T恤49件,乙种T恤51件时获利最大,最大利润为3510元.


科目:初中数学 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
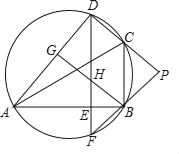
【题目】如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=![]() DH,∠COD=23°,求∠P的度数.
DH,∠COD=23°,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
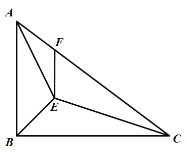
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的![]() 位居民,得到这
位居民,得到这![]() 位居民一周内使用共享单车的次数分别为:
位居民一周内使用共享单车的次数分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)这组数据的中位数是________,众数是________;
(2)计算这![]() 位居民一周内使用共享单车的平均次数;
位居民一周内使用共享单车的平均次数;
(3)若该小区有![]() 名居民,试估计该小区居民一周内使用共享单车的总次数.
名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com