【题目】如图，一次函数y1=kx+b的图象与反比例函数y2=
的图象交于A（2，3），B（6，n）两点．
（1）分别求出一次函数与反比例函数的解析式；
（2）求△OAB的面积．
【答案】(1) 反比例函数的解析式为y=
，一次函数的解析式为y=﹣
x+4．(2)8.
【解析】
（1）根据反比例函数y2=
的图象过点A（2，3），利用待定系数法求出m，进而得出B点坐标，然后利用待定系数法求出一次函数解析式；
（2）设直线y1=kx+b与x轴交于C，求出C点坐标，根据S△AOB=S△AOC﹣S△BOC，列式计算即可．
（1）∵反比例函数y2=的图象过A（2，3），B（6，n）两点，∴m=2×3=6n，∴m=6，n=1，∴反比例函数的解析式为y=，B的坐标是（6，1）．
把A（2，3）、B（6，1）代入y1=kx+b，得：
，解得：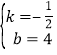
，∴一次函数的解析式为y=﹣x+4．
（2）如图，设直线y=﹣x+4与x轴交于C，则C（8，0）．
S△AOB=S△AOC﹣S△BOC=×8×3﹣×8×1=12﹣4=8．
名校通行证有效作业系列答案科目：初中数学 来源： 题型：
【题目】（1）如图，在由边长为1的正方形组成的网络纸中有四边形
.
①利用网格作出边
的垂直平分线
、
的垂直平分线
；
②设①中、两条直线交于点
，连接
、
、
，判断：_____，_____（用“
”、“
”或“
”填空）；
③在直线上取点
，使得
值最小.
（2）在由边长为1的正方形组成的网格纸中，已知线段
、
，请在网格纸中分别画出两个不同的
，使得
，高
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在下列的网格图中.每个小正方形的边长均为1个单位，在Rt△ABC中，∠C=90°，AC=3，BC=4.
(1)试在图中作出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；
(2)若点B的坐标为(-3，5)，试在图中画出直角坐标系，并标出A、C两点的坐标；
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2，并标出B2、C2两点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列等式：①1=12；②2+3+4=32；③3+4+5+6+7=52；④4+5+6+7+8+9+10=72；…请根据上述规律判断下列等式正确的是（ ）
A. 1008+1009+…+3025=20162 B. 1009+1010+…+3026=20172
C. 1009+1010+…+3025=20172 D. 1010+1011+…+3029=20192
查看答案和解析>>
科目：初中数学 来源： 题型：
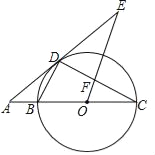
【题目】如图，BC为⊙O的直径，点D在⊙O上，连结BD、CD，过点D的切线AE与CB的延长线交于点A，∠BCD=∠AEO，OE与CD交于点F．
（1）求证：OF∥BD；
（2）当⊙O的半径为10，sin∠ADB=
时，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．
（1）求证：AD=AG；
（2）AD与AG的位置关系如何，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+
x+c过A（﹣1，0），B（0，2）两点．
（1）求抛物线的解析式．
（2）M为抛物线对称轴与x轴的交点，N为x轴上对称轴上任意一点，若tan∠ANM=
，求M到AN的距离．
（3）在抛物线的对称轴上是否存在点P，使△PAB为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中折线表示y与x之间的函数关系，根据图象进行以下探究：
信息获取：
（1）甲、乙两地之间的距离为 km
（2）请解释图中点B的实际意义；图象理解： .
（3）求慢车和快车的速度；
（4）求出C点的坐标．
（第（3）、（4）问要求写出求解过程）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
