
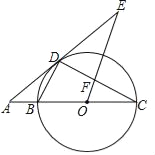
【题目】如图,BC为⊙O的直径,点D在⊙O上,连结BD、CD,过点D的切线AE与CB的延长线交于点A,∠BCD=∠AEO,OE与CD交于点F.
(1)求证:OF∥BD;
(2)当⊙O的半径为10,sin∠ADB=![]() 时,求EF的长.
时,求EF的长.
【答案】(1)证明见解析;(2)EF=21.
【解析】
(1)连接OD,如图,利用切线的性质得到OD⊥AE,利用圆周角定理得到∠BDC=90°,然后证明∠ADB=∠AEO得到BD∥OF;
(2)由(1)知,sin∠C=sin∠E=sin∠ADB=![]() .在Rt△BCD中,利用正弦的定义计算出BD=8,再利用三角形中位线性质得到OF=
.在Rt△BCD中,利用正弦的定义计算出BD=8,再利用三角形中位线性质得到OF=![]() BD=4,接着在Rt△EOD中利用正弦定义计算出OE=25,然后计算OE与OF的差即可.
BD=4,接着在Rt△EOD中利用正弦定义计算出OE=25,然后计算OE与OF的差即可.
(1)连接OD,如图,∵AE与O相切,∴OD⊥AE,∴∠ADB+∠ODB=90°.
∵BC为直径,∴∠BDC=90°,即∠ODB+∠ODC=90°,∴∠ADB=∠ODC.
∵OC=OD,∴∠ODC=∠C,而∠BCD=∠AEO,∴∠ADB=∠AEO,∴BD∥OF;
(2)由(1)知,∠ADB=∠E=∠BCD,∴sin∠C=sin∠E=sin∠ADB=![]() .在Rt△BCD中,sin∠C=
.在Rt△BCD中,sin∠C=![]() =
=![]() ,∴BD=
,∴BD=![]() ×20=8.
×20=8.
∵OF∥BD,∴OF=![]() BD=4.在Rt△EOD中,sin∠E=
BD=4.在Rt△EOD中,sin∠E=![]() =
=![]() ,∴OE=25,∴EF=OE﹣OF=25﹣4=21.
,∴OE=25,∴EF=OE﹣OF=25﹣4=21.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
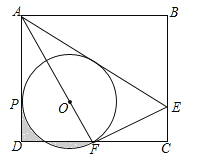
【题目】(2017四川省达州市,第16题,3分)如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④
CE;④![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k-1)x+k2=0有两个实根x1和x2
(1) 求实数k的取值范围
(2) 若方程两实根x1、x2满足x12-x22=0,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,4),B(8,0),C(8,4),连接AC,BC得到四边形AOBC,点D在边AC上,连接OD,将边OA沿OD折叠,点A的对应点为点P,若点P到四边形AOBC较长两边的距离之比为1:3,则点P的坐标为__________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.
(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
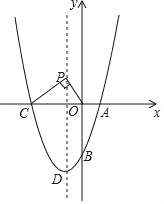
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、C两点,点A在点C的右边,与y轴交于点B,点B的坐标为(0,﹣3),且OB=OC,点D为该二次函数图象的顶点.
(1)求这个二次函数的解析式及顶点D的坐标;
(2)如图,若点P为该二次函数的对称轴上的一点,连接PC、PO,使得∠CPO=90°,请求出所有符合题意的点P的坐标;
(3)在对称轴上是否存在一点P,使得∠OPC为钝角,若存在,请直接写出点P的纵坐标为yp的取值范围,若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
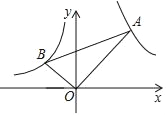
【题目】如图,在x轴的上方,直角∠BOA绕原点O按顺时针方向旋转,若∠BOA的两边分别与函数y=﹣![]() ,y=
,y=![]() 的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
的图象交于B、A两点,则tan∠OAB的值的变化趋势为( )
A. 逐渐变小 B. 逐渐变大 C. 时大时小 D. 保持不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com