解:(1)-1
2012+
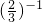
+(π-3)
0-(-2)
-2
=-1+

+1-

=

;
(2)2m
2•(-2mn)•(-

m
3n
3)
=2×(-2)×(-

)m
2+1+3•n
1+3
=2m
6n
4;
(3)(-x
3)
2+(-x
2)
3-x•x
5
=(-1)
2•(x
3)
2+(-1)
3•(x
2)
3-x
1+5
=x
6-x
6-x
6
=-x
6;
(4)k(k+7)-(k-3)(k+2)
=k
2+7k-(k
2+2k-3k-6)
=k
2+7k-k
2-2k+3k+6
=8k+6;
(5)(3x-2y)
2-(2y-3x)(3x+2y)
=(9x
2-12xy+4y
2)-(6xy+4y
2-9x
2-6xy)
=9x
2-12xy+4y
2-6xy-4y
2+9x
2+6xy
=18x
2-12xy;
(6)(2a-b+3)(2a+b-3)
=[2a-(b-3)][2a+(b-3)]
=(2a)
2-(b-3)
2
=4a
2-(b
2-6b+9)
=4a
2-b
2+6b-9.
分析:(1)原式第一项-1
2012表示1的2012次幂的相反数,第二、四项根据负指数公式a
-p=

(a≠0)计算,第三项利用零指数公式a
0=1(a≠0)计算,把所得的结果相加减,即可得到最后结果;
(2)利用单项式乘以单项式的法则:系数相乘,同底数幂相乘,只在一个单项式中出现的字母,连同它的指数作为积的一个因式,然后利用同底数幂的乘法法则计算后,即可得到结果;
(3)根据幂的乘方运算法则:底数不变指数相乘将原式的前两项进行计算,最后一项利用同底数幂的乘法法则:底数不变指数相加进行计算,合并同类项后即可得到结果;
(4)先利用单项式乘以多项式,以及多项式乘以多项式的法则将原式进行计算,去括号合并同类项后,即可得到结果;
(5)原式第一项利用完全平方公式展开,第二项利用多项式乘以多项式的法则计算,去括号合并同类项后即可得到结果;
(6)将原式变形后,利用平方差公式化简,再利用积的乘方及完全平方公式变形,去括号后即可得到结果.
点评:此题考查了整式的混合运算,涉及的知识有:同底数幂的乘方、除法运算,零指数、负指数公式,单项式乘以单项式,单项式乘以多项式,以及多项式乘以多项式的法则,以及平方差公式、完全平方公式的运用,熟练掌握公式及法则是解本题的关键.

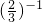 +(π-3)0-(-2)-2
+(π-3)0-(-2)-2  m3n3)
m3n3)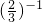 +(π-3)0-(-2)-2
+(π-3)0-(-2)-2 +1-
+1-
 ;
; m3n3)
m3n3) )m2+1+3•n1+3
)m2+1+3•n1+3 (a≠0)计算,第三项利用零指数公式a0=1(a≠0)计算,把所得的结果相加减,即可得到最后结果;
(a≠0)计算,第三项利用零指数公式a0=1(a≠0)计算,把所得的结果相加减,即可得到最后结果;
