
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.

【答案】见解析
【解析】试题分析:(1)、根据AB=AC可得∠B=∠C,根据DE⊥AB,DF⊥AC可得∠BED=∠CFD=90°,根据D为中点可得BD=CD,根据AAS可以判定三角形全等;(2)、根据三个角为直角的四边形是矩形,首先得出矩形,然后根据(1)的结论说明有一组邻边相等.
试题解析:(1)、∵AB=AC ∴∠B=∠C ∵DE⊥AB,DF⊥AC ∴∠BED=∠CFD=90°
∵D为BC的中点 ∴BD=CD ∴△BED≌△CFD
(2)、∵DE⊥AB,DF⊥AC ∴∠AED=∠AFD=90° 又∵∠A=90°
∴四边形DFAE为矩形 ∵△BED≌△CFD ∴DE=DF ∴四边形DFAE为正方形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象.
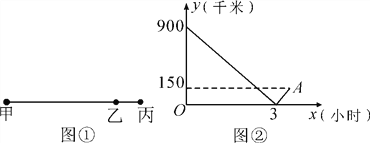
(1)填空:甲、丙两地距离_______千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州市体育中考项目改为耐力跑后,某体育用品商场预测某款运动鞋能够畅销,就用16000元购进了一批这款运动鞋,上市后很快脱销,商场又用40000元购进第二批这款运动鞋,所购数量是第一批的2倍,但每双鞋的进价高了10元.求该款运动鞋第一次进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=![]() .
.

(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度;
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知空气的单位体积质量是0.001239g/cm3,则用科学记数法表示该数为( )
A. 1.239×10﹣3g/cm3 B. 1.239×10﹣2g/cm3
C. 0.1239×10﹣2g/cm3 D. 12.39×10﹣4g/cm3
查看答案和解析>>
科目:初中数学 来源: 题型:
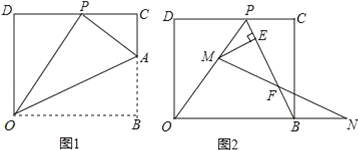
【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.
(1)如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各对量中,不具有相反意义的是( )
A.胜3局与负3局
B.收入3000元与增加3000元
C.气温升高4℃与气温降低10℃
D.转盘逆时针转3圈与顺时针转5圈
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com