
【题目】如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象.
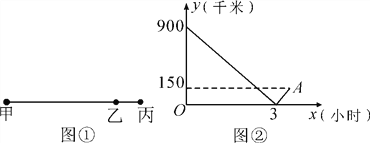
(1)填空:甲、丙两地距离_______千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.
【答案】(1) 1050;(2)y=![]() .
.
【解析】试题分析:(1)根据函数图形可得,甲、丙两地距离为:900+150=1050(千米);
(2)分两种情况:当0≤x≤3时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=kx+b,把(0,900),(3,0)代入得到方程组,即可解答;根据确定高速列出的速度为300(千米/小时),从而确定点A的坐标为(3.5,150),当3<x≤3.5时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=k1x+b1,把(3,0),(3.5,150)代入得到方程组,即可解答.
试题解析:解:(1)根据函数图形可得,甲、丙两地距离为:900+150=1050(千米),故答案为:900.
(2)当0≤x≤3时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=kx+b,
把(0,900),(3,0)代入得:![]() ,
,
解得:![]() ,
,
∴y=﹣300x+900,
高速列出的速度为:900÷3=300(千米/小时),
150÷300=0.5(小时),3+0.5=3.5(小时)
如图2,点A的坐标为(3.5,150)
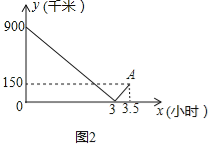
当3<x≤3.5时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=k1x+b1,
把(3,0),(3.5,150)代入得:![]() ,
,
解得: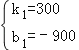 ,
,
∴y=300x﹣900,
∴y=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列各式由左边到右边的变形中,是因式分解的是( )
A. 2xy+6xz+3=2x(y+3z)+3 B. (x+6)(x﹣6)=x2﹣36
C. ﹣2x2﹣2xy=﹣2x(x+y) D. 3a2﹣3b2=3(a2﹣b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正比例函数y=2x的图像与一次函数 y=kx+b的图像交于点A(m,2),一次函数的图像经过点B(-2,-1)与y轴交点为C与x轴交点为D.
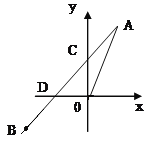
(1)求一次函数的解析式;
(2)求C点的坐标;
(3)求△AOD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
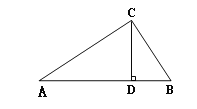
(1)求DC的长;
(2)求AB的长;
(3)求证:△ABC是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学前,李浩去商场买书包,商场在搞促销活动,买一个书包可以通过抽奖形式送笔.方法如下:在一个不透明的箱子里,分别装有四张完全一样的卡片,上面分别写有“钢笔”、 “圆珠笔”、“铅笔”、“谢谢”字样(其中“谢谢”卡即意味着没有奖品).凭抽取的卡片,工作人员即时对应地给出奖品.李浩买了一个书包,并参加了抽奖.
(1)若只准抽一次,且每次只能抽一张,直接写出李浩能抽到一支笔的概率;
(2)若可以不放回地抽两次,每次只能抽一张,请用树形图把所有可能的情况表示出来,并求李浩得到钢笔和圆珠笔的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )

A. 20×(![]() )4030 B. 20×(
)4030 B. 20×(![]() )4032 C. 20×(
)4032 C. 20×(![]() )2016 D. 20×(
)2016 D. 20×(![]() )2015
)2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com