
【题目】如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
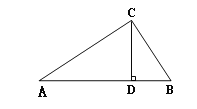
(1)求DC的长;
(2)求AB的长;
(3)求证:△ABC是直角三角形.
【答案】(1)12;(2)25;(3)证明见解析.
【解析】试题分析:(1)在RT△BCD中运用勾股定理即可求出CD的长;
(2)在RT△ACD中运用勾股定理即可求出AD的长;
(3)已知△ABC的三边,根据勾股定理的逆定理即可判定△ABC是直角三角形.
试题解析:(1)在RT△BCD中,∵∠CDB=90°,BC=15,BD=9,
∴CD=![]() =12;
=12;
(2)在RT△ACD中,∵∠CDA=90°,AC=20,CD=12,
∴AD=![]() =16
=16
所以AB=AD+DB=25;
(3)在△ABC中,∵AC=20,BC=15,AB=AD+DB=16+9=25,
∴AC2+BC2=400+225=625=252=AB2,
∴△ABC是直角三角形.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP和△ECP相似的是( )

A. ∠APB=∠EPC B. ∠APE=90° C. BP:BC=2:3 D. P是BC中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数m=162-3x.
(1)写出商场卖这种商品每天的销售利润y(元)与每件的销售价x(元)间的函数关系式;
(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最为合适?最大销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象.
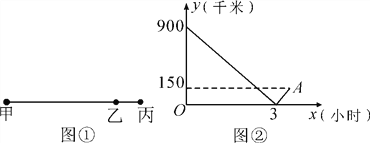
(1)填空:甲、丙两地距离_______千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点(3,2)。
的图象经过点(3,2)。
(1)求这个二次函数的关系式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当x>0时,求使y≥2的x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=![]() .
.

(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度;
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com