
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊA(0ЃЌm)ЁЂB(nЃЌ0)ЃЌЧв|mЉnЉ3|+![]() ЃН0ЃЌЕуPДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃН0ЃЌЕуPДгAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOдШЫйдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
(1)ЧѓOAЁЂOBЕФГЄЃЛ
(2)СЌНгPBЃЌЩшЁїPOBЕФУцЛ§ЮЊSЃЌгУtЕФЪНзгБэЪОSЃЛ
(3)Й§ЕуPзїжБЯпABЕФДЙЯпЃЌДЙзуЮЊDЃЌжБЯпPDгыxжсНЛгкЕуEЃЌдкЕуPдЫЖЏЕФЙ§ГЬжаЃЌЪЧЗёДцдкетбљЕФЕуPЃЌЪЙЁїEOPЁеЁїAOBЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1)OA=6ЃЌOB=3ЃЛ(2)SЃН![]() |6Љt|(tЁн0)ЃЛ(3)tЃН3Лђ9ЃЎ
|6Љt|(tЁн0)ЃЛ(3)tЃН3Лђ9ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЫуЪѕЦНЗНИљКЭОјЖджЕЕФЗЧИКаджЪМДПЩЧѓЕУmЁЂnЕФжЕЃЌМДПЩНтЬтЃЛ
ЃЈ2ЃЉСЌНгPBЃЌtУыКѓЃЌПЩЧѓЕУOPЃН6ЉtЃЌМДПЩЧѓЕУSЕФжЕЃЛ
ЃЈ3ЃЉзїГіЭМаЮЃЌвзжЄЁЯOBAЃНЁЯOPEЃЌжЛвЊOPЃНOBЃЌМДПЩЧѓжЄЁїEOPЁеЁїAOBЃЌЗжСНжжЧщаЮЧѓЕУtЕФжЕЃЌМДПЩНтЬтЃЎ
(1)Ёп|mЉnЉ3|+![]() ЃН0ЃЌ
ЃН0ЃЌ
Чв|mЉnЉ3|Ён0ЃЌ![]() Ён0
Ён0
Ёр|mЉnЉ3|ЃН![]() ЃН0ЃЌ
ЃН0ЃЌ
ЁрnЃН3ЃЌmЃН6ЃЌ
ЁрЕуA(0ЃЌ6)ЃЌЕуB(3ЃЌ0)ЃЛ
(2)СЌНгPBЃЌ

tУыКѓЃЌAPЃНtЃЌOPЃН|6Љt|ЃЌ
ЁрSЃН![]() OPOBЃН
OPOBЃН![]() |6Љt|ЃЛ(tЁн0)
|6Љt|ЃЛ(tЁн0)
(3)зїГіЭМаЮЃЌ

ЁпЁЯOAB+ЁЯOBAЃН90ЁуЃЌЁЯOAB+ЁЯAPDЃН90ЁуЃЌЁЯOPEЃНЁЯAPDЃЌ
ЁрЁЯOBAЃНЁЯOPEЃЌ
ЁржЛвЊOPЃНOBЃЌМДПЩЧѓжЄЁїEOPЁеЁїAOBЃЌ
ЁрAPЃНAOЉOPЃН3ЃЌЛђAPЁфЃНOA+OPЁфЃН9
ЁрtЃН3Лђ9ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКЁЯ1+ЁЯ2ЃН180ЁуЃЌЁЯBЃНЁЯDЃЌCDЦНЗжЁЯACFЃЎ
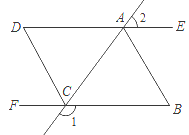
ЃЈ1ЃЉDEгыBFЦНааТ№ЃПЧыЫЕУїРэгЩЃЎ
ЃЈ2ЃЉABгыCDЮЛжУЙиЯЕШчКЮЃПЮЊЪВУДЃП
ЃЈ3ЃЉABЦНЗжЁЯCAEТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуOЮЊе§ЗНаЮABCDЕФжааФЃЌBEЦНЗжЁЯDBCНЛDCгкЕуEЃЌбгГЄBCЕНЕуFЃЌЪЙFC=ECЃЌСЌНсDFНЛBEЕФбгГЄЯпгкЕуHЃЌСЌНсOHНЛDCгкЕуGЃЌСЌНсHCЃЎдђвдЯТЫФИіНсТлжаЃКЂйOHЁЮBFЃЌЂкGH=![]() BCЃЌЂлBF=2ODЃЌЂмЁЯCHF=45ЁуЃЎе§ШЗНсТлЕФИіЪ§ЮЊ( )
BCЃЌЂлBF=2ODЃЌЂмЁЯCHF=45ЁуЃЎе§ШЗНсТлЕФИіЪ§ЮЊ( )

A.4ИіB.3ИіC.2ИіD.1Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ХзЮяЯпy=ax2+bx+c(aЁй0)ОЙ§Еу ОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ5ЃЌЉ6ЃЉЃЌCЃЈ6ЃЌ0ЃЉ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌдкжБЯпABЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуPЪЙЫФБпаЮPACBЕФУцЛ§зюДѓЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЕуQЮЊХзЮяЯпЕФЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЪджИГіЁїQABЮЊЕШбќШ§НЧаЮЕФЕуQвЛЙВгаМИИіЃПВЂЧыЧѓГіЦфжаФГвЛИіЕуQЕФзјБъ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ A(0ЃЌa)ЃЌB(bЃЌ0)ЃЌaЁЂb Тњзу.a+b=4ЃЌa-b= 12ЃЌ
ЃЈ1ЃЉЧѓ aЁЂb ЕФжЕЃЛ
ЃЈ2ЃЉдкзјБъжсЩЯеввЛЕу DЃЌЪЙШ§НЧаЮ ABD ЕФУцЛ§ЕШгкШ§НЧаЮ OAB УцЛ§ЕФвЛАыЃЌ Чѓ D ЕузјБъЃЛ
ЃЈ3ЃЉзїЁЯBAO ЦНЗжЯпгыЁЯABC ЦНЗжЯп BE ЕФЗДЯђбгГЄЯпНЛгк P ЕуЃЌЧѓЁЯP ЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁЯAOB=90Ёу,ЕуCЁЂDЗжБ№дкЩфЯпOAЁЂOBЩЯЃЌЕуEдкЁЯAOBФкВП.
ЃЈ1ЃЉИљОнгяОфЛЭМаЮЃК
ЂйЛжБЯпCEЃЛ
ЂкЛЩфЯпOEЃЛ
ЂлЛЯпЖЮDEЃЌ
ЃЈ2ЃЉНсКЯЭМаЮЃЌЭъГЩЯТУцЕФЬюПеЃК
ЂйгыЁЯODEЛЅВЙЕФНЧЪЧ ЃЛ
ЂкШєЁЯBOE =![]() ЁЯAOEЃЌдђЁЯBOEЕФДѓаЁЪЧ .
ЁЯAOEЃЌдђЁЯBOEЕФДѓаЁЪЧ .

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќЁїABCжаЃЌЕуDЁЂEЗжБ№ЪЧБпABЁЂACЩЯЕФСНЕуЃЈЕуDВЛгыЕуAЁЂ ЕуBжиКЯЃЉЃЌЧвDEЁЮBCЃЌвдDEЮЊвЛБпЃЌдкЫФБпаЮDBCEЕФФкВПзїе§ЗНаЮDEFGЃЌвбжЊAB=AC=5ЃЌBC=6ЃЎ
ЃЈ1ЃЉЪдЧѓЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉЕБGFгыBCжиКЯЪБЃЌЧѓе§ЗНаЮDEFGЕФБпГЄЃЛ
ЃЈ3ЃЉШєBGЕФГЄЖШЕШгке§ЗНаЮDEFGЕФБпГЄЃЌЪдЧѓADЕФГЄЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌВЂгУЯрЙиЕФЫМЯыЗНЗЈНтОіЮЪЬтЃЎ
МЦЫуЃКЃЈ1Љ![]() Љ
Љ![]() Љ
Љ![]() ЃЉЁСЃЈ
ЃЉЁСЃЈ![]() +
+![]() +
+![]() ЃЉЉЃЈ1Љ
ЃЉЉЃЈ1Љ![]() Љ
Љ![]() Љ
Љ![]() ЃЉЁСЃЈ
ЃЉЁСЃЈ![]() +
+![]() +
+![]() ЃЉЃЎ
ЃЉЃЎ
Сю![]() +
+![]() +
+![]() =tЃЌдђдЪН=ЃЈ1ЉtЃЉЃЈt+
=tЃЌдђдЪН=ЃЈ1ЉtЃЉЃЈt+![]() ЃЉЉЃЈ1ЉtЉ
ЃЉЉЃЈ1ЉtЉ![]() ЃЉt=t+
ЃЉt=t+![]() Љt2Љ
Љt2Љ![]() tЉ
tЉ![]() t+t2=
t+t2=![]() ЃЌ
ЃЌ
ЮЪЬтЃК
ЃЈ1ЃЉМЦЫуЃКЃЈ1Љ![]() Љ
Љ![]() Љ
Љ![]() ЃЉЁСЃЈ
ЃЉЁСЃЈ![]() +
+![]() +
+![]() ЃЉЉЃЈ1Љ
ЃЉЉЃЈ1Љ![]() Љ
Љ![]() Љ
Љ![]() ЃЉЁСЃЈ
ЃЉЁСЃЈ![]() +
+![]() +
+![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉНтЗНГЬЃЈx2+5x+1ЃЉЃЈx2+5x+7ЃЉ=7ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌГЄЗНаЮABCDЕФБпABдкyжсе§АыжсЩЯЃЌЖЅЕуAЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌЩшЖЅЕуCЕФзјБъЮЊЃЈaЃЌbЃЉЃЎ
ЃЈ1ЃЉЖЅЕуBЕФзјБъЮЊЁЁ ЃЌЖЅЕуDЕФзјБъЮЊЁЁ ЃЈгУaЛђbБэЪОЃЉЃЛ
ЃЈ2ЃЉШчЙћНЋвЛИіЕуЕФКсзјБъзїЮЊxЕФжЕЃЌзнзјБъзїЮЊyЕФжЕЃЌДњШыЗНГЬ2x+3yЃН12ГЩСЂЃЌОЭЫЕетИіЕуЕФзјБъЪЧЗНГЬ2x+3yЃН12ЕФНтЃЎвбжЊЖЅЕуBКЭDЕФзјБъЖМЪЧЗНГЬ2x+3yЃН12ЕФНтЃЌЧѓaЃЌbЕФжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЦНвЦГЄЗНаЮABCDЃЌЪЙЕуBвЦЖЏЕНЕуDЃЌЕУЕНаТЕФГЄЗНаЮEDFGЃЌ
ЂйетДЮЦНвЦПЩвдПДГЩЪЧЯШНЋГЄЗНаЮABCDЯђгвЦНвЦЁЁ ИіЕЅЮЛГЄЖШЃЌдйЯђЯТЦНвЦЁЁ ИіЕЅЮЛГЄЖШЕФСНДЮЦНвЦЃЛ
ЂкШєЕуPЃЈmЃЌnЃЉЪЧЖдНЧЯпBDЩЯЕФвЛЕуЃЌЧвЕуPЕФзјБъЪЧЗНГЬ2x+3yЃН12ЕФНтЃЌЪдЫЕУїЦНвЦКѓЕуPЕФЖдгІЕуPЁфЕФзјБъвВЪЧЗНГЬ2x+3yЃН12ЕФНтЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com