
【题目】如图所示,∠AOB=90°,点C、D分别在射线OA、OB上,点E在∠AOB内部.
(1)根据语句画图形:
①画直线CE;
②画射线OE;
③画线段DE,
(2)结合图形,完成下面的填空:
①与∠ODE互补的角是 ;
②若∠BOE =![]() ∠AOE,则∠BOE的大小是 .
∠AOE,则∠BOE的大小是 .

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,OC平分∠AOB,点P是射线OC上的一点.
,OC平分∠AOB,点P是射线OC上的一点.

(1)如图一,过点P作PD⊥OA,PE⊥OB,说明PD与PE相等的理由.
(2)如图二,如果点F、G分别在射线OA、OB上,且∠FPG=60°,那么线段PF与PG相等吗?请说明理由;
(3)在(2)的条件下,联合FG,![]() 是什么形状的三角形,请说明理由.
是什么形状的三角形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两个袋中均装有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的三个数值为﹣7,﹣1,3.乙袋中的三张卡片上所标的数值为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上的数值,把x,y分别作为点A的横坐标和纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
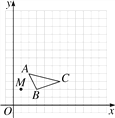
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣3|+![]() =0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外都相同的红球和黄球,两种颜色的球一共有10个,每次摸出其中一个球,记下颜色后,放回搅匀.一个同学进行了反复试验,下面是做该试验获得的数据.
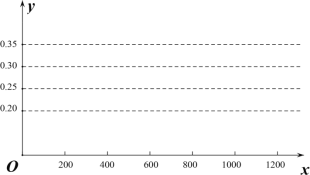
(1)a= ,画出摸到红球的频率的折线统计图;
(2)从这个袋子中任意摸一个球,摸到黄球的概率估计值是多少?(精确到0.1)
(3)怎样改变袋中红球或黄球的个数,可以使得任意摸一次,摸到两种颜色球的概率相等?(写出一种方案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BAC中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
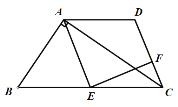
(1)求证:DC=EC.
(2)若AB=6,BC=10,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D, 其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,当a=![]() 时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
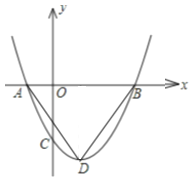
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com