
����Ŀ����һ�������Ĵ�����װ�г���ɫ�ⶼ��ͬ�ĺ���ͻ���������ɫ����һ����10����ÿ����������һ��������ɫ�Żؽ��ȣ�һ��ͬѧ�����˷������飬���������������õ����ݣ�
��1��a= ���������������Ƶ�ʵ�����ͳ��ͼ��
��2�������������������һ������������ĸ��ʹ���ֵ�Ƕ��٣�����ȷ��0.1��
��3�������ı���к�������ĸ���������ʹ��������һ�Σ�����������ɫ��ĸ�����ȣ���д��һ�ַ������ɣ�
���𰸡���1��![]() ����2��ԼΪ0.7����3������4��������õ�4�����𰸲�Ψһ��
����2��ԼΪ0.7����3������4��������õ�4�����𰸲�Ψһ��
��������
��1����������ֻҪ��348����1200����a��ֵ�������ɻ������������Ƶ�ʵ�����ͳ��ͼ��
��2���ɱ������ݿɵ�����������ʵĹ���ֵ�������ɵ���������ĸ��ʹ���ֵ��
��3������ǰ��ȷ�������к���ͻ���ĸ�������������x�����������y�������������г����̣��ⷽ�̼��ɵó����ۣ�
�⣺��1��348��1200=0.29����![]() ��
��
���������Ƶ�ʵ�����ͳ��ͼ��ͼ��ʾ��
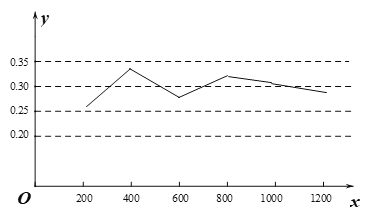
��2��������ã�����������ʵĹ���ֵΪ0.3��������������ĸ��ʹ���ֵ=1��0.3=0.7��
��3�����ڴ������к���3��������7������������x��������![]() ����ã�x=4��
����ã�x=4��
��������y��������![]() ����ã�y=4��
����ã�y=4��
��������4��������õ�4�����𰸲�Ψһ��������ʹ��������һ�Σ�����������ɫ��ĸ�����ȣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫƽ����ʽ����a��b��2��a2��2ab+b2�ʵ��ı��Σ����Խ���ܶ����ѧ���⣮
���磺��a+b��3��ab��1����a2+b2��ֵ��
�⣺��Ϊa+b��3��ab��1
���ԣ�a+b��2��9��2ab��2
����a2+b2+2ab��9��2ab��2
��a2+b2��7
��������Ľ���˼·�뷽��������������⣺
��1������7��x����x��4����1����7��x��2+��x��4��2��ֵ��
��2����ͼ����C���߶�AB�ϵ�һ�㣬��AC��BCΪ���������������Σ���AB��5���������ε������S1+S2��17����ͼ����Ӱ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC��һ�㣬����OB��OC������AB��OB��OC��AC���е�D��E��F��G�������ᣬ�õ��ı���DEFG��

��1����֤���ı���DEFG��ƽ���ı��Σ�
��2�������OBC=45������OCB=30����OC=4����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ۿ�A�ڹ۲�վO����������OA=4km��ij���Ӹۿ�A�������ر�ƫ��15��������һ�ξ����B������ʱ�ӹ۲�վO����øô�λ�ڱ�ƫ��60���ķ�����ô����еľ��루��AB�ij�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����AOB=90��,��C��D�ֱ�������OA��OB�ϣ���E�ڡ�AOB�ڲ�.
��1��������仭ͼ�Σ�
�ٻ�ֱ��CE��
�ڻ�����OE��
�ۻ��߶�DE��
��2�����ͼ�Σ�����������գ�
�����ODE�����Ľ��� ��
������BOE =![]() ��AOE�����BOE�Ĵ�С�� .
��AOE�����BOE�Ĵ�С�� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y=![]() x2ƽ�Ƶõ�������m��������m������A����6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������y=
x2ƽ�Ƶõ�������m��������m������A����6��0����ԭ��O��0��0�������Ķ���ΪP�����ĶԳ�����������y=![]() x2���ڵ�Q����ͼ����Ӱ���ֵ����Ϊ________��
x2���ڵ�Q����ͼ����Ӱ���ֵ����Ϊ________��
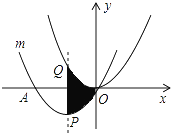
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E�DZ�AD��һ�㣬��AE=AB��
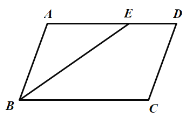
��1������BCD�Ľ�ƽ����CF����AD��F�㣬��BE��G�㣻���߹���ͼ�������ۼ�����д������
��2���ڣ�1���������£�
�����BGC�Ķ�����
����AB=a��BC=b�����߶�EF= ���ú�a,b��ʽ�ӱ�ʾ����
����AB=10��CF=12����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ίԱͳ����ȫ��ͬѧ60�������Ĵ���,���г������Ƶ���ֲ�
���� | 60��x<80 | 80��x<100 | 100��x<120 |
Ƶ�� | 1 | 2 | 25 |
���� | 120��x<140 | 140��x<160 | 160��x<180 |
Ƶ�� | 15 | 5 | 2 |
(1)ȫ���ж���ѧ��?
(2)����Ƕ���?�����Ƕ���
(3)��������x��100��x<140��Χ��ѧ��ռȫ��ѧ���İٷ�֮��?
(4)�����ʵ���ͳ��ͼ��ʾ�������Ϣ.
(5)���������������������ɼ�?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
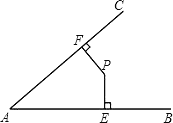
����Ŀ����ͼ��ʾ��P�ǡ�BAC�ڵ�һ�㣬PE��AB��PF��AC������ֱ�Ϊ��E��F��AE=AF����֤��
��1��PE=PF��
��2����P�ڡ�BAC��ƽ�����ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com