
【题目】如图,在□ABCD中,点E是边AD上一点,且AE=AB.
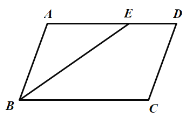
(1)作∠BCD的角平分线CF,交AD于F点,交BE于G点;(尺规作图,保留痕迹,不写画法)
(2)在(1)的条件下,
①求∠BGC的度数;
②设AB=a,BC=b,则线段EF= (用含a,b的式子表示);
③若AB=10,CF=12,求BE的长.
【答案】(1)见解析;(2)①90°;②![]() ;③
;③ ![]()
【解析】
(1)以点D为圆心,DC为半径作圆交AD于点F,连接CF交BE于点G即为所作;
(2)①根据角平分线的定义和平行线的性质,就可求出;
②根据角平分线的定义和平行线的性质可得出DC=DF,再因为AB=AE即可求出;
③根据平行线+角平分线可推出等腰三角形,进而可证得四边形AHCF是平行四边形,因为∠BGC=90°可得∠AMB=90°,所以点M是BE的中点也是AH的中点,再根据勾股定理可求出BM的值,即可求出答案.
(1)如下图所示:
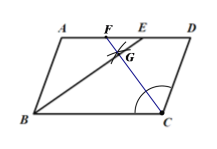
此图即为所作.
(2)①∵AB=AE,
∴∠ABE=∠AEB,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ABC+∠BCD=180°,
∴∠AEB=∠CBE,
∴∠ABE=∠CBE=![]() ∠ABC,
∠ABC,
∵CF平分∠BCD,
∴∠BCF=![]() ∠BCD,
∠BCD,
∴∠CBE+∠BCF=90°,
∴∠BGC=180°-90°=90°
②∵CF平分∠BCD,
∴∠BCF=∠DCF
∵AD∥BC,
∴∠BCF=∠DFC,
∴∠DFC=∠DCF,
∴DF=DC,
∵AB=a,BC=b,
∴EF=![]() ,
,
③作∠BAD的平分线交BC于点H,交BE于点M,如下图所示:
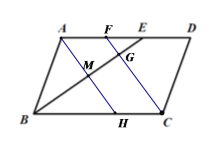
∵AH平分∠BAD,
∴∠BAH=∠DAH,
∵AD∥BC,
∴∠BAH=∠AHB,
∴AB=BH,△ABH是等腰三角形,
∵DC=DF,
∴BH=DF
∴HC=BC-BH=AD-DF=AF,
∵AD∥BC,
∴四边形AHCF是平行四边形,
∴AH∥CF,
∴∠BMH=∠BGC=90°,
∴点M是AH的中点,
∵AB=AE,
∴△ABE是等腰三角形,
∴点M是BE的中点,
∵AB=10,CF=12,
∴AH=CF=10,
∴AM=6,
在△AMB中,由勾股定理得:
![]() ,
,
∴BE=16.


科目:初中数学 来源: 题型:
【题目】作图与探究(不写作法,保留作图痕迹,并用 0.5 毫米黑色签字笔描深痕迹) 如图,∠DBC 和∠ECB 是△ABC 的两个外角°
(1)用直尺和圆规分别作∠DBC 和∠ECB 的平分线,设它们相交于点 P;
(2)过点 P 分别画直线 AB、AC、BC 的垂线段 PM、PN、PQ,垂足 为 M、N、Q;
(3) PM、PN、PQ 相等吗?(直接写出结论,不需说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
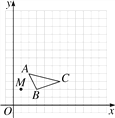
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外都相同的红球和黄球,两种颜色的球一共有10个,每次摸出其中一个球,记下颜色后,放回搅匀.一个同学进行了反复试验,下面是做该试验获得的数据.
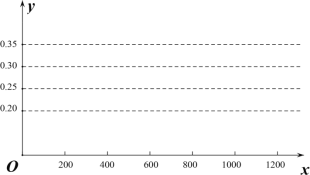
(1)a= ,画出摸到红球的频率的折线统计图;
(2)从这个袋子中任意摸一个球,摸到黄球的概率估计值是多少?(精确到0.1)
(3)怎样改变袋中红球或黄球的个数,可以使得任意摸一次,摸到两种颜色球的概率相等?(写出一种方案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BAC中,∠BAC=90°,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.
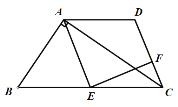
(1)求证:DC=EC.
(2)若AB=6,BC=10,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C是x轴的正半轴上从左向右依次排列的三点,过点A,B,C分别作与![]() 轴平行的直线
轴平行的直线![]() ,
,![]() ,
,![]() .
.
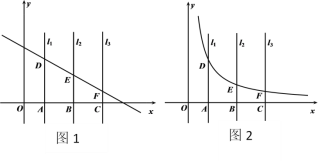
(1)如图1,若直线![]() 与直线
与直线![]() ,
,![]() ,
,![]() 分别交于点D,E,F三点,设D(
分别交于点D,E,F三点,设D(![]() ,
,![]() ),E(
),E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ) .
) .
①若![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() (填“=”,“>”或“<”);
(填“=”,“>”或“<”);
②若![]() ,
,![]() ,
,![]() (
(![]() ),求证:AB=BC;
),求证:AB=BC;
(2)如图2,点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),直线
),直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,根据以上探究的经验,探索
)的图像分别交于点D,E,F,根据以上探究的经验,探索
![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高![]() 米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心
米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为米处达到最高,水柱落地处离池中心![]() 米.
米.

(1)请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;
(2)求出水柱的最大高度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com