
【题目】在平面直角坐标系中,点A,B,C是x轴的正半轴上从左向右依次排列的三点,过点A,B,C分别作与![]() 轴平行的直线
轴平行的直线![]() ,
,![]() ,
,![]() .
.
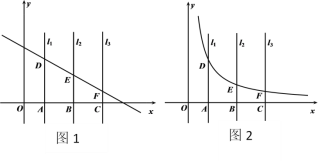
(1)如图1,若直线![]() 与直线
与直线![]() ,
,![]() ,
,![]() 分别交于点D,E,F三点,设D(
分别交于点D,E,F三点,设D(![]() ,
,![]() ),E(
),E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ) .
) .
①若![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() (填“=”,“>”或“<”);
(填“=”,“>”或“<”);
②若![]() ,
,![]() ,
,![]() (
(![]() ),求证:AB=BC;
),求证:AB=BC;
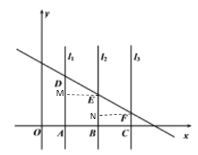
(2)如图2,点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),直线
),直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,根据以上探究的经验,探索
)的图像分别交于点D,E,F,根据以上探究的经验,探索
![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
【答案】(1)①见解析;②见解析;(2)![]()
【解析】
(1)①根据点D、E、F的横坐标证得AB=BC=1,过点E作EM⊥AD,过点F作FN⊥BE,证明△DME≌△ENF,得到DM=EN,即可推出![]() ,由此得到答案;
,由此得到答案;
②过点E作EM⊥AD,过点F作FN⊥BE,得到![]() ,
,![]() ,根据
,根据![]() ,
,![]() ,
,![]() (
(![]() ),证得DM=EN,证明△DME≌△ENF即可推出AB=BC;
),证得DM=EN,证明△DME≌△ENF即可推出AB=BC;
(2)连接直线DF交直线![]() 于G,根据点A,B,C的横坐标分别为
于G,根据点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),得到AB=BC,D(n-1,
),得到AB=BC,D(n-1,![]() ),E(n,
),E(n,![]() ),F(n+1,
),F(n+1,![]() ),由(1)得到
),由(1)得到![]() ,由直线
,由直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,求得
)的图像分别交于点D,E,F,求得![]() ,
,![]() ,根据点G的纵坐标大于点E的纵坐标,点E的纵坐标为
,根据点G的纵坐标大于点E的纵坐标,点E的纵坐标为![]() ,得到
,得到![]() ,即可推出
,即可推出![]() .
.
(1)①∵D(1,![]() ),E(2,
),E(2,![]() ),F(3,
),F(3,![]() ),且过点A,B,C分别作与
),且过点A,B,C分别作与![]() 轴平行的直线
轴平行的直线![]() ,
,![]() ,
,![]() ,
,
∴A(1,0),B(2,0),C(3,0),
∴AB=BC=1,
过点E作EM⊥AD,过点F作FN⊥BE,
∴∠DME=ENF=90°,
∵![]() ∥
∥![]() ,
,
∴∠EDM=∠FEN,
∴△DME≌△ENF,
∴DM=EN,
∴![]() ,
,
∴![]() ,
,
故答案为:=;
②过点E作EM⊥AD,过点F作FN⊥BE,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,![]() (
(![]() ),
),
∴DM=2,EN=2,
∴DM=EN,
∵![]() ∥
∥![]() ,
,
∴∠EDM=∠FEN,
∵∠DME=ENF=90°,
∴△DME≌△ENF,
∴AB=BC;
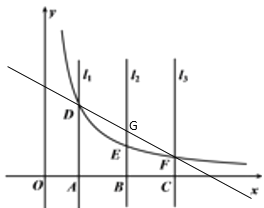
(2)![]() ,
,
连接直线DF交直线![]() 于G,
于G,
∵点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),
),
∴点D,G,F的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),AB=BC,
),AB=BC,
∴D(n-1,![]() ),E(n,
),E(n,![]() ),F(n+1,
),F(n+1,![]() ) ,
) ,
∴![]() ,
,
∵直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,
)的图像分别交于点D,E,F,
∴![]() ,
,![]() ,
,
又∵点G的纵坐标大于点E的纵坐标,点E的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知 CD 是经过∠BCA 顶点 C 的一条直线,CA=CB.E、F 分别是直线 CD 上两点(不 重合),且∠BEC=∠CFA=∠a
(1)若直线 CD 经过∠BCA 的内部,且 E、F 在射线 CD 上,请解决下面问题:
①若∠BCA=90°,∠a=90°,请在图 1 中补全图形,并证明:BE=CF,EF=![]() ;
;
②如图 2,若 0°<∠BCA<180°,请添加一个关于∠a 与∠BCA 关系的条件 , 使①中的两个结论仍然成立;
(2)如图 3,若直线 CD 经过∠BCA 的外部,∠a=∠BCA,请写出 EF、BE、AF 三条线 段数量关系(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,求该船航行的距离(即AB的长).

查看答案和解析>>
科目:初中数学 来源: 题型:
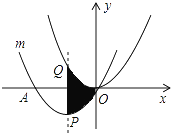
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为________.
x2交于点Q,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是边AD上一点,且AE=AB.
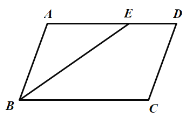
(1)作∠BCD的角平分线CF,交AD于F点,交BE于G点;(尺规作图,保留痕迹,不写画法)
(2)在(1)的条件下,
①求∠BGC的度数;
②设AB=a,BC=b,则线段EF= (用含a,b的式子表示);
③若AB=10,CF=12,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个计算装置示意图,A、B是数据输入口,C是计算输出口,计算过程是由A、B分别输入自然数m和n,经计算后得自然数K由C输出,此种计算装置完成的计算满足以下三个性质:
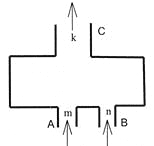
(1)若A、B分别输入1,则输出结果为1;
(2)若A输入任何固定的自然数不变,B输入自然数增大1,则输出结果比原来增大2;
(3)若B输入任何固定的自然数不变,A输入自然数增大1,则输出结果为原来的2倍。
试问:(1)若A输入1,B输入自然数4,输出结果为 。
(2)若B输入1,A输入自然数5,输出结果为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布
次数 | 60≤x<80 | 80≤x<100 | 100≤x<120 |
频数 | 1 | 2 | 25 |
次数 | 120≤x<140 | 140≤x<160 | 160≤x<180 |
频数 | 15 | 5 | 2 |
(1)全班有多少学生?
(2)组距是多少?组数是多少
(3)跳绳次数x在100≤x<140范围的学生占全班学生的百分之几?
(4)画出适当的统计图表示上面的信息.
(5)你怎样评价这个班的跳绳成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们规定:点![]() 关于“
关于“![]() 的衍生点”,
的衍生点”,![]() ,其中
,其中![]() 为常数且
为常数且![]() ,如:点
,如:点![]() (
(![]() ,
,![]() )关于“
)关于“![]() 的衍生点”,即
的衍生点”,即![]() ,即
,即![]() .
.
(1)求点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() 的坐标;
的坐标;
(2)若点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,点
,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,且线段
,且线段![]() 的长度不超过线段
的长度不超过线段![]() 长度的一半,请问:是否存在
长度的一半,请问:是否存在![]() 值使得
值使得![]() 到
到![]() 轴的距离是
轴的距离是![]() 到
到![]() 轴距离的
轴距离的![]() 倍?若存在,请求出
倍?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com