【题目】要设计一幅宽20cm，长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2∶3，如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？
【答案】每个横、竖彩条的宽度分别为
cm、
cm.
【解析】试题分析：设每个横彩条的宽为2xcm，则每个竖彩条的宽为3xcm．求出剩余部分的面积，根据剩余部分的面积是原图案面积的
列方程求解即可．
试题解析：
解:设每个横彩条的宽为2xcm，则每个竖彩条的宽为3xcm．
∴剩余部分的宽为：(20－6x)cm，剩余部分的长为：(30－4x)cm，
∴剩余部分矩形的面积为：(20－6x)(30－4x)＝24x2－260x＋600（cm2）.
根据题意，得24x2－260x＋600＝(1－
)×20×30.
整理，得6x2－65x＋50＝0.
解方程，得x1＝
，x2＝10，
∵x2＝10不合题意，舍去.
∴x＝
.
则2x＝
，3x＝
．
答：每个横、竖彩条的宽度分别为
cm、
cm.
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A，B，C是x轴的正半轴上从左向右依次排列的三点，过点A，B，C分别作与
轴平行的直线
，
，
．
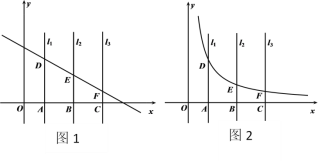
（1）如图1，若直线
与直线，，分别交于点D，E，F三点，设D（
，
），E（
，
），F（
，
） ．
①若
，
，
，则
（填“=”，“>”或“<”）；
②若
，
，
（
），求证：AB=BC；
（2）如图2，点A，B，C的横坐标分别为
，n，
（
），直线，，与反比例函数
（
）的图像分别交于点D，E，F，根据以上探究的经验，探索
与
之间的大小关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间？
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
查看答案和解析>>
科目：初中数学 来源： 题型：
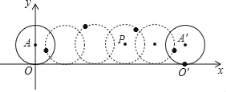
【题目】如图，在平面直角坐标系中，半径为1的圆从原点出发沿x轴正方向滚动一周，圆上一点由原点O到达点O′，圆心也从点A到达点A′．
（1）点O′的坐标为 ，点A′的坐标为 ；
（2）若点P是圆在滚动过程中圆心经过的某一位置，求以点P，点O，点O′为顶点的三角形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了加强学生的安全意识，某校组织了学生参加安全知识竞赛，从中抽取了部分学生成绩进行统计，并按照成绩从低到高分成A，B，C，D，E五个小组，绘制统计图如下（未完成），解答下列问题：
（1）样本容量为 ，频数分布直方图中a＝ ；
（2）扇形统计图中D小组所对应的扇形圆心角为n°，求n的值并补全频数分布直方图；
（3）若成绩在80分以上（不含80分）为优秀，全校共有2000名学生，估计成绩优秀的学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中有Rt△ABC，∠BAC=90°，AB=AC，A（3，0），B（0，1）
（1）将△ABC沿x轴的正方向平移t个单位，B、C两点的对应点B′、C′正好落在反比例函数y=
的图象上．请直接写出C点的坐标和t，k的值；
（2）有一个Rt△DEF，∠D=90°，∠E=60°，DE=2，将它放在直角坐标系中，使斜边EF在x轴上，直角顶点D在（1）中的反比例函数图象上，求点F的坐标；
（3）在（1）的条件下，问是否存在x轴上的点M和反比例函数y=图象上的点N，使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在，直接写出所有满足条件的点M和点N的坐标；如果不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：我们把
称为二阶行列式，规定它的运算法则为＝ad﹣bc，例如：
＝2×5﹣3×4＝﹣2．
（1）填空：若
＝0，则x＝ ，
＞0，则x的取值范围 ；
（2）若对于正整数m，n满足，1
＜3，求m+n的值；
（3）若对于两个非负数x，y，
＝
＝k﹣1，求实数k的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
