练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN，BE⊥MN，垂足分别为点D，E．求证：DE＝AD＋BE．

    【答案】见解析

    【解析】

    根据垂直定义求出∠BEC=∠ACB=∠ADC，根据等式性质求出∠ACD=∠CBE，根据AAS证出△ADC和△CEB全等，可推出CD=BE，AD=CE，进而可证明DE=AD+BE．

    证明：如图,∵∠ACB=90°，AD⊥MN，BE⊥MN，

    ∴∠BEC=∠ACB=∠ADC=90°，

    ∴∠ACD +∠BCE=90°,∠BCE+∠CBE=90°，

    ∴∠ACD=∠CBE，

    在△ADC和△CEB中，

    ∠ADC=∠BEC，∠ACD=∠CBE，AC=BC，

    ∴△ADC≌△CEB(AAS)；

    ∴BE=CD，AD=CE，

    ∵CD+CE=DE，

    ∴DE=AD+BE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．

    （1）证明：AF=CE；

    （2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知 CD 是经过∠BCA 顶点 C 的一条直线，CA＝CB．E、F 分别是直线 CD 上两点（不 重合），且∠BEC＝∠CFA＝∠a

    (1)若直线 CD 经过∠BCA 的内部，且 E、F 在射线 CD 上，请解决下面问题：

    ①若∠BCA＝90°，∠a＝90°，请在图 1 中补全图形，并证明：BE＝CF，EF＝；

    ②如图 2，若 0°<∠BCA<180°，请添加一个关于∠a 与∠BCA 关系的条件 ， 使①中的两个结论仍然成立；

    (2)如图 3，若直线 CD 经过∠BCA 的外部，∠a＝∠BCA，请写出 EF、BE、AF 三条线 段数量关系（不要求证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC在直角坐标系中，

    （1）请写出△ABC各点的坐标.

    （2）求出△ABC的面积.

    （3）若把△ABC向上平移2个单位，再向右平移2个单位得△A′B′C′，在图中画出△ABC变化位置。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．

    （1）求证：四边形DEFG是平行四边形；

    （2）如果∠OBC=45°，∠OCB=30°，OC=4，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，相邻两条平行直线间的距离相等，若等腰直角三角形ABC的直角顶点C在上，另两个顶点A、B分别在、上，则的值是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，求该船航行的距离（即AB的长）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

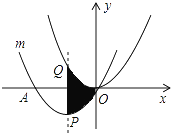
    【题目】如图，把抛物线y=x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=x2交于点Q，则图中阴影部分的面积为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】要设计一幅宽20cm，长30cm的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为2∶3，如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？

    查看答案和解析>>

    同步练习册答案