
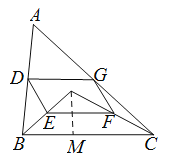
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF =![]() BC,DG∥BC且DG =
BC,DG∥BC且DG =![]() BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)过点O作OM⊥BC于M,由∠OCM=30°,OC=4,得到OM=![]() OC =2,从而得到CM=
OC =2,从而得到CM=![]() ,在Rt△OBM中,由∠BMO=∠OMB=45°,得到BM=OM=2,故BC=
,在Rt△OBM中,由∠BMO=∠OMB=45°,得到BM=OM=2,故BC=![]() ,从而有EF=
,从而有EF=![]() .
.
试题解析:(1)∵ D、G分别是AB、AC的中点,∴DG∥BC,DG=![]() BC,∵ E、F分别是OB、OC的中点,∴EF∥BC,EF=
BC,∵ E、F分别是OB、OC的中点,∴EF∥BC,EF=![]() BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;
BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;
(2)过点O作OM⊥BC于M,Rt△OCM中,∠OCM=30°,OC=4,∴OM=![]() OC =2,∴CM=
OC =2,∴CM=![]() ,Rt△OBM中,∠BMO=∠OMB=45°,∴BM=OM=2,∴BC=
,Rt△OBM中,∠BMO=∠OMB=45°,∴BM=OM=2,∴BC=![]() ,∴EF=
,∴EF=![]() .
.


科目:初中数学 来源: 题型:
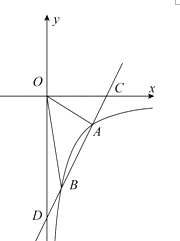
【题目】如图,在平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() (
(![]() 且
且![]() )交于
)交于![]() 、
、![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,连接
两点,连接![]() 、
、![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3s后,两点相距15个单位长度.已知动点A、B的速度比是1:4(速度单位:单位长度/s).![]()
(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3s时的位置;
(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒时,原点恰好处在两个动点的正中间?
(3)在(2)中原点恰好处在两个动点的正中间时,A、B两点同时向数轴负方向运动,另一动点C和点B同时从点B位置出发向A运动,当遇到A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/s的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a=﹣2,|b|=0,(c﹣12)2与|d﹣18|互为相反数.![]()
(1)b=;c=;d= .
(2)若A、B两点以2个单位长度/秒的速度向右匀速运动,同时C、D两点以1个单位长度/秒的速度向左匀速运动,并设运动时间为t秒,问t为多少时,A、C两点相遇?
(3)在(2)的条件下,A、B、C、D四点继续运动,当点B运动到点D的右侧时,问是否存在时间t,使得B与D的距离是C与D的距离的3倍?若存在,求时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.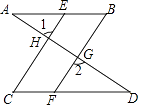
证明:∵AB∥CD(已知)
∴∠B=().
∵∠B=∠C(已知)
∴∠BFD=∠C()
∴∥()
∴∠2=(两直线平行,同位角相等)
∵∠1=()
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示,A、B、C三点的坐标分别为A(﹣1,3)、B(﹣4,1)、C(﹣2,1),把△ABC向右平移4个单位长度后得到对应的△A1B1C1 , 再将△A1B1C1向下平移5个单位长度后得到对应的△A2B2C2 . 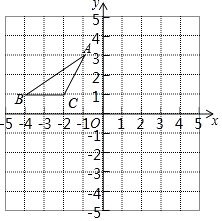
(1)分别作出△A1B1C1和△A2B2C2;
(2)求△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠AGE,∠D=∠1,且∠1+∠2=180°,则下列结论:①CE∥BF,②∠A=∠D,③AB∥CD,④∠C=∠B,其中正确的结论有( )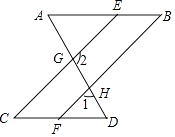
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com