
【题目】如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.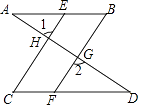
证明:∵AB∥CD(已知)
∴∠B=().
∵∠B=∠C(已知)
∴∠BFD=∠C()
∴∥()
∴∠2=(两直线平行,同位角相等)
∵∠1=()
∴∠1=∠2(等量代换).
【答案】∠BFD;两直线平行,内错角相等;等量代换;BC;BF;同位角相等,两直线平行;∠CHG;∠CHG;对顶角相等
【解析】证明:∵AB∥CD(已知)
∴∠B=∠BFD(两直线平行,内错角相等).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴BC∥BF(同位角相等,两直线平行)
∴∠2=∠CHG(两直线平行,同位角相等)
∵∠1=∠CHG(对顶角相等)
∴∠1=∠2(等量代换).
故答案是:∠BFD; 两直线平行,内错角相等; 等量代换;BC;BF;∠CHG;∠CHG; 对顶角相等.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】画图题: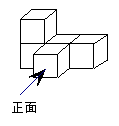

(1)由大小相同的小立方块搭成的几何体如左图,请在右图的方格中画出该几何体的俯视图和左视图。
(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在右图方格中所画的图一致,则这样的几何体最少要个小立方块,最多要个小立方块。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由5个大小相同的小正方体拼成的几何体如图所示,则下列说法正确的是( )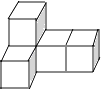
A.主视图的面积最小
B.左视图的面积最小
C.俯视图的面积最
D.三个视图的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的骰子六个面分别刻有1到6的点数,掷两次骰子,得到向上一面的两个点数,则下列事件中,发生可能性最大的是( )
A.点数都是偶数
B.点数的和为奇数
C.点数的和小于13
D.点数的和小于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把文字翻译成数学符号,构建方程组模型是解此类题的关键某超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表统计了近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800 |
第二周 | 6台 | 8台 | 3180 |
(1)求A、B两种型号的电风扇每台的销售价分别是多少元?
(2)若超市准备用不超过5250元的金额再采购这两种型号的电风扇共30台,
①求A种型号的电风扇最多能采购多少台?
②超市销售完这30台电风扇是否能实现利润不低于1240元的目标?若能实现,请写出相应的采购方案,若不能实现,请说明理由.
(进价、售价均保持不变,利润=销售收入﹣进货成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学科内综合题:现把10个数:﹣1,23,15,12,0,﹣31,﹣11,29,43,﹣62.分别写在10张纸条上,然后把纸条放进外形,颜色完全相同的小球内,再把这10个小球放进一个大玻璃瓶中,从中任意取一球,得到正数的可能性与得到负数的可能性哪个大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某现代农业示范园区准备租用甲、乙两种货车将一批蔬菜运到城区销售,已知一辆甲种货车可装茄子4吨和玉米1吨,一辆乙种货车可装茄子和玉米各2吨,若园区要求安排甲,乙两种货车共10辆一次性运输茄子和玉米,其中茄子不少于30吨,玉米不少于13吨.
(1)那么园区如何安排甲,乙两种货车进行运输?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费280元,则园区应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com