
【题目】某现代农业示范园区准备租用甲、乙两种货车将一批蔬菜运到城区销售,已知一辆甲种货车可装茄子4吨和玉米1吨,一辆乙种货车可装茄子和玉米各2吨,若园区要求安排甲,乙两种货车共10辆一次性运输茄子和玉米,其中茄子不少于30吨,玉米不少于13吨.
(1)那么园区如何安排甲,乙两种货车进行运输?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费280元,则园区应选择哪种方案,使运输费最少?最少运费是多少?
【答案】
(1)解:设安排甲种货车x辆,则安排乙种货车(10﹣x)辆,依题意得
![]() ,
,
解此不等式组得5≤x≤7.
∵x是正整数
∴x可取的值为5,6,7.
∴安排甲、乙两种货车有三种方案:
甲种货车 | 乙种货车 | |
方案一 | 5辆 | 5辆 |
方案二 | 6辆 | 4辆 |
方案三 | 7辆 | 3辆 |
(2)解:∵甲种货车每辆要付运输费300元,乙种货车每辆要付运输费280元,
∴选择方案一运费最少,最少运费是300×5+280×5=2900(元).
答:园区应选择方案一,使运输费最少,最少运费是2900元
【解析】(1)由题意列出不等式组,在解集内有几个整数解就有几种方案;(2)由已知算出每种方案的费用,比较得出最少运费方案.
【考点精析】根据题目的已知条件,利用一元一次不等式组的应用的相关知识可以得到问题的答案,需要掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠B=∠C,求证:∠1=∠2.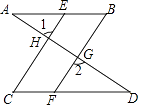
证明:∵AB∥CD(已知)
∴∠B=().
∵∠B=∠C(已知)
∴∠BFD=∠C()
∴∥()
∴∠2=(两直线平行,同位角相等)
∵∠1=()
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级三位老师带部分学生去红色旅游,联系了甲、乙两家旅行社,甲旅行社说:“老师免费,学生打八折。”乙旅行社说:“包括老师在内全部打七折.”若全程费用为每人200元,求:
(1)设有 x 名学生参加活动,请分别写出参加两家旅行社的费用的代数式;
(2)若有25名学生参加活动,问选择哪家旅行社更合算?
(3)分别计算21名和15名学生参加活动时两家旅行社的费用?根据上面的结果应如何选择哪家旅行社更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( ) 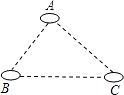
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com