
【题目】已知 CD 是经过∠BCA 顶点 C 的一条直线,CA=CB.E、F 分别是直线 CD 上两点(不 重合),且∠BEC=∠CFA=∠a
(1)若直线 CD 经过∠BCA 的内部,且 E、F 在射线 CD 上,请解决下面问题:
①若∠BCA=90°,∠a=90°,请在图 1 中补全图形,并证明:BE=CF,EF=![]() ;
;
②如图 2,若 0°<∠BCA<180°,请添加一个关于∠a 与∠BCA 关系的条件 , 使①中的两个结论仍然成立;
(2)如图 3,若直线 CD 经过∠BCA 的外部,∠a=∠BCA,请写出 EF、BE、AF 三条线 段数量关系(不要求证明).

【答案】(1)①见解析;②添加条件:∠α+∠ACB=180°时,①中两个结论仍然成立,证明见解析;(2)EF=BE+AF..
【解析】
(1)①求出∠BEC=∠AFC=90°,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;
②求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可.
(2)求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可.
(1)①如图1中,
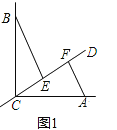
E点在F点的左侧,∵BE⊥CD,AF⊥CD,∠ACB=90°,
∴∠BEC=∠AFC=90°,
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
 ,
,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
证明:如图2中,.
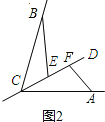 .
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
 ,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】已知射线![]() 平行于射线
平行于射线![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上.
上.

(1)如图1,若点![]() 在线段
在线段![]() 上,若
上,若![]() ,
,![]() 时,则
时,则![]() _________.
_________.
(2)如图1,若点![]() 在线段
在线段![]() 上运动(不包含
上运动(不包含![]() 、
、![]() 两点),则
两点),则![]() 、
、![]() 、
、![]() 之间的等量关系是_____________________.
之间的等量关系是_____________________.
(3)①如图2,若点![]() 在线段
在线段![]() 的延长线上运动,则
的延长线上运动,则![]() 、
、![]() 、
、![]() 之间的等量关系是________________;
之间的等量关系是________________;
②如图3,若点![]() 在线段
在线段![]() 的延长线上运动,则
的延长线上运动,则![]() 、
、![]() 、
、![]() 之间的等量关系是________________.
之间的等量关系是________________.
(4)请说明图2中所得结论的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
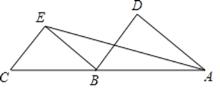
【题目】已知A,B,C三点在同一直线上,∠DAE=∠AEB,∠D=∠BEC,
(1)求证:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图与探究(不写作法,保留作图痕迹,并用 0.5 毫米黑色签字笔描深痕迹) 如图,∠DBC 和∠ECB 是△ABC 的两个外角°
(1)用直尺和圆规分别作∠DBC 和∠ECB 的平分线,设它们相交于点 P;
(2)过点 P 分别画直线 AB、AC、BC 的垂线段 PM、PN、PQ,垂足 为 M、N、Q;
(3) PM、PN、PQ 相等吗?(直接写出结论,不需说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图,△ABC中,AB=AC,且∠A=36°.

(1)在图中用尺规作边AB的垂直平分线交AC于D,连接BD(保留作图痕迹,不写作法).
(2)请问△BDC是不是黄金三角形,如果是,请给出证明,如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:
![]() 如图1,已知:在
如图1,已知:在![]() 中,
中,![]() ,
,![]() ,直线m经过点A,
,直线m经过点A,![]() 直线m,
直线m,![]() 直线m,垂足分别为点D、
直线m,垂足分别为点D、![]() 试猜想DE、BD、CE有怎样的数量关系,请直接写出;
试猜想DE、BD、CE有怎样的数量关系,请直接写出;
![]() 组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将
组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将![]() 中的条件改为:在
中的条件改为:在![]() 中,
中,![]() ,D、A、E三点都在直线m上,并且有
,D、A、E三点都在直线m上,并且有![]() 其中
其中![]() 为任意锐角或钝角
为任意锐角或钝角![]() 如果成立,请你给出证明;若不成立,请说明理由.
如果成立,请你给出证明;若不成立,请说明理由.
![]() 数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
如图3,F是![]() 角平分线上的一点,且
角平分线上的一点,且![]() 和
和![]() 均为等边三角形,D、E分别是直线m上A点左右两侧的动点
均为等边三角形,D、E分别是直线m上A点左右两侧的动点![]() 、E、A互不重合
、E、A互不重合![]() ,在运动过程中线段DE的长度始终为n,连接BD、CE,若
,在运动过程中线段DE的长度始终为n,连接BD、CE,若![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B,C是x轴的正半轴上从左向右依次排列的三点,过点A,B,C分别作与![]() 轴平行的直线
轴平行的直线![]() ,
,![]() ,
,![]() .
.
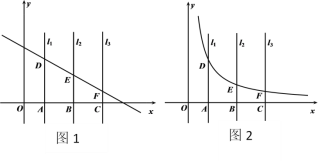
(1)如图1,若直线![]() 与直线
与直线![]() ,
,![]() ,
,![]() 分别交于点D,E,F三点,设D(
分别交于点D,E,F三点,设D(![]() ,
,![]() ),E(
),E(![]() ,
,![]() ),F(
),F(![]() ,
,![]() ) .
) .
①若![]() ,
,![]() ,
,![]() ,则
,则![]()
![]() (填“=”,“>”或“<”);
(填“=”,“>”或“<”);
②若![]() ,
,![]() ,
,![]() (
(![]() ),求证:AB=BC;
),求证:AB=BC;
(2)如图2,点A,B,C的横坐标分别为![]() ,n,
,n,![]() (
(![]() ),直线
),直线![]() ,
,![]() ,
,![]() 与反比例函数
与反比例函数![]() (
(![]() )的图像分别交于点D,E,F,根据以上探究的经验,探索
)的图像分别交于点D,E,F,根据以上探究的经验,探索
![]() 与
与![]() 之间的大小关系,并说明理由.
之间的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com