
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(3,0),B(0,1)

(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=![]() 的图象上.请直接写出C点的坐标和t,k的值;
的图象上.请直接写出C点的坐标和t,k的值;
(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
(3)在(1)的条件下,问是否存在x轴上的点M和反比例函数y=![]() 图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
【答案】(1)C(4,3),t=6,k=6;(2)满足条件的点F的坐标为(![]() 3,0)或(
3,0)或(![]() +3,0);(3)存在,点N(3,2),M(7,0)时,四边形MNC′B′是平行四边形,当N′(3,2),M(7,0)时,四边形M′N′B′C′是平行四边形
+3,0);(3)存在,点N(3,2),M(7,0)时,四边形MNC′B′是平行四边形,当N′(3,2),M(7,0)时,四边形M′N′B′C′是平行四边形
【解析】
(1)过C点作CH⊥x轴,构造△CAH≌△ABO,从而确定C点坐标,根据坐标平移规律沿x轴的正方向平移t个单位可得B′(t、1)、C′(-4+t,3),根据反比例函数性质可求出t,然后可求出k;
(2)分情况画出斜边在x轴,直角顶点D在反比例图象上,先求出直角三角形斜边的高,即D点的y值,即可解决问题.
(3)分两种情形:①线段B′C′为平行四边形的边时.②线段B′C′是对角线时,分别求解即可.
(1)如图1中,过C点作CH⊥x轴,垂足为H,
∵∠BAC=∠AOB=∠CHA=90°,
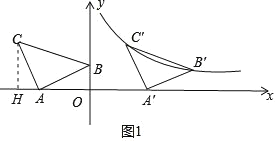
∴∠CAH+∠BAO=90°,∠BAO+∠ABO=90°,
∴∠CAH=∠ABO,
∵AC=AB,
∴△CHA≌△AOB(AAS),
∴AH=OB=1,OA=CH=3,
∴C(4,3),B(0,1),
由题意![]() (4+t,3),
(4+t,3),![]() (t,1),
(t,1),
∵![]() ,
,![]() 都在y=
都在y=![]() 上,
上,
∴(4+t)×3=t×1,
∴t=6,
∴![]() (6,1),
(6,1),
∴k=6.
(2)如图2中,作DH⊥x轴于H.
在Rt△DEF中,∵∠EDF=90°,∠DEF=60°,DE=2,
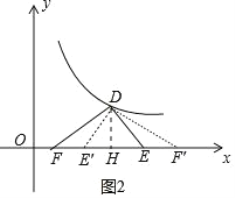
∴EF=4,DF=![]() ,
,
∵![]() DFDE=
DFDE=![]() EFDH,
EFDH,
∴DH=![]() ,
,
∴FH=3,EH=1,D(![]() ,
,![]() ),
),
∴OF=![]() 3,
3,
∴F(![]() 3,0),
3,0),
当点![]() 在点
在点![]() 右侧时,
右侧时,![]() (
(![]() +3,0).
+3,0).
综上所述,满足条件的点F的坐标为(![]() 3,0)或(
3,0)或(![]() +3,0).
+3,0).
(3)由(1)可知:![]() (6,1),
(6,1),![]() (2,3).
(2,3).

当点N(3,2),M(7,0)时,四边形![]() 是平行四边形,
是平行四边形,
当![]() (3,2),M(7,0)时,四边形
(3,2),M(7,0)时,四边形![]() 是平行四边形.
是平行四边形.


科目:初中数学 来源: 题型:
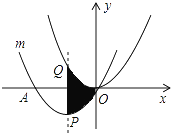
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为________.
x2交于点Q,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要设计一幅宽20cm,长30cm的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2∶3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,应如何设计每个彩条的宽度?

查看答案和解析>>
科目:初中数学 来源: 题型:
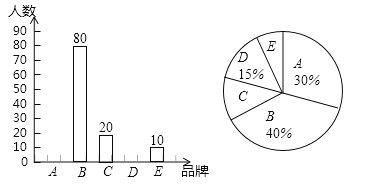
【题目】“共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
(1)求出本次参与调查的市民人数;
(2)将上面的条形图补充完整;
(3)若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩托单车出行?
查看答案和解析>>
科目:初中数学 来源: 题型:
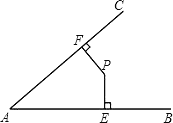
【题目】如图所示,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
(1)PE=PF;
(2)点P在∠BAC的平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用“=”、“>”、“<”填空
![]()
![]() ; 6+3
; 6+3 ![]() ;
;![]()
![]() ;7+7
;7+7 ![]() ;
;
(2)由(1)中各式猜想a+b与![]() 的大小,并说明理由.
的大小,并说明理由.
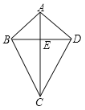
(3)请利用上述结论解决下面问题:
某同学在做一个面积为1800cm2,对角线互相垂直的四边形风筝时,求用来做对角线的竹条至少要多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们规定:点![]() 关于“
关于“![]() 的衍生点”,
的衍生点”,![]() ,其中
,其中![]() 为常数且
为常数且![]() ,如:点
,如:点![]() (
(![]() ,
,![]() )关于“
)关于“![]() 的衍生点”,即
的衍生点”,即![]() ,即
,即![]() .
.
(1)求点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() 的坐标;
的坐标;
(2)若点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,点
,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,且线段
,且线段![]() 的长度不超过线段
的长度不超过线段![]() 长度的一半,请问:是否存在
长度的一半,请问:是否存在![]() 值使得
值使得![]() 到
到![]() 轴的距离是
轴的距离是![]() 到
到![]() 轴距离的
轴距离的![]() 倍?若存在,请求出
倍?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE//AC,且DE:AC=1:2,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com