
【题目】已知:如图,∠A=∠ADE,∠C=∠E.

(1)求证:BE∥CD;
(2)若∠EDC=3∠C,求∠C的度数.
【答案】(1)详见解析;(2)∠C=45°.
【解析】
(1)根据“内错角相等,两直线平行”得到DE∥AC,再根据平行线的性质得到∠E=∠ABE,利用等量代换根据平行线的判定即可得证;
(2)根据“两直线平行,同旁内角互补”可得∠EDC+∠C=180°,利用等量代换求解即可.
(1)证明:∵∠A=∠ADE,
∴DE∥AC(内错角相等,两直线平行),
∴∠E=∠ABE(两直线平行,内错角相等),
∵∠E=∠C,
∴∠ABE=∠C,
∴BE∥CD(同位角相等,两直线平行).
(2)解:∵DE∥AC,
∴∠EDC+∠C=180°(两直线平行,同旁内角互补),
∵∠EDC=3∠C,
∴4∠C=180°,
∴∠C=45°.


科目:初中数学 来源: 题型:
【题目】张翔上午7:30出发,从学校骑自行车去县城,路程全长20km,中途因道路施工步行一段路.他步行的平均速度是5km/h
(1)若张翔骑车的平均速度是15km/h,当天上午9:00到达县城,则他骑车与步行各用多少时间?
(2)若张翔必须在当天上午9:00之前赶到县城,他的步行平均速度不变,则他骑车的平均速度应在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(3,0),B(0,1)

(1)将△ABC沿x轴的正方向平移t个单位,B、C两点的对应点B′、C′正好落在反比例函数y=![]() 的图象上.请直接写出C点的坐标和t,k的值;
的图象上.请直接写出C点的坐标和t,k的值;
(2)有一个Rt△DEF,∠D=90°,∠E=60°,DE=2,将它放在直角坐标系中,使斜边EF在x轴上,直角顶点D在(1)中的反比例函数图象上,求点F的坐标;
(3)在(1)的条件下,问是否存在x轴上的点M和反比例函数y=![]() 图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′、M、N为顶点的四边形构成平行四边形?如果存在,直接写出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,E为对角线BD的延长线上一点.

(1)求证:AE=CE.
(2)若BC=6,AE=10,∠BAE=120,求BE的长,并直接写出DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在给定的一张平行四边形纸片上按如下操作:连结AC,作AC的垂直平分线MN分别交AD、AC、BC于M、O、N,连结AN,CM,则四边形ANCM是( )

A. 矩形 B. 菱形 C. 正方形 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:我们把![]() 称为二阶行列式,规定它的运算法则为
称为二阶行列式,规定它的运算法则为![]() =ad﹣bc,例如:
=ad﹣bc,例如:![]() =2×5﹣3×4=﹣2.
=2×5﹣3×4=﹣2.
(1)填空:若![]() =0,则x= ,
=0,则x= ,![]() >0,则x的取值范围 ;
>0,则x的取值范围 ;
(2)若对于正整数m,n满足,1![]() <3,求m+n的值;
<3,求m+n的值;
(3)若对于两个非负数x,y,![]() =
=![]() =k﹣1,求实数k的取值范围.
=k﹣1,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5![]() 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
(2)如图2,矩形ABCD中,AB=![]() ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF![]() DE于点F,若DE=
DE于点F,若DE=![]() CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;
(3)如图3,在Rt![]() ABC中,
ABC中,![]() ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
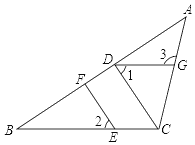
(1)试说明DG∥BC的理由;
(2)如果∠B=34°,且∠ACD=47°,求∠3的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com