
【题目】如图,菱形ABCD中,E为对角线BD的延长线上一点.

(1)求证:AE=CE.
(2)若BC=6,AE=10,∠BAE=120,求BE的长,并直接写出DE的长为 .
【答案】(1)见解析;(2)BE=11,![]() .
.
【解析】
(1)由菱形的性质得出AB=CB,∠ABE=∠CBE,证明△ABE≌△CBE,即可得出结论;
(2)连接AC交BD于O,作EF⊥BA延长线于点F,先求AF,EF的长度,再根据勾股定理求出BE长,证明△AOB∽△EFB,从而求出BO长,即可求出DE的长度.
解:(1)∵四边形ABCD是菱形,
∴AB=CB,∠ABE=∠CBE,
在△ABE和△CBE中
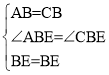
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)连接AC交BD于O,作EF⊥BA延长线于点F,如图所示:
∵∠BAE=120°,
∴∠EAF=180°-∠BAE=60°,
∴∠AEF=90°-60°=30°,
∵AE=10,
∴AF=![]() ,
,
∴![]() ,
,
∵BC=6,
∴BA=BC=6,
∴BF=11,
∴![]() ,
,
∵四边形ABCD为菱形,
∴AC⊥BD,
∴△AOB∽△EFB,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.



 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,是一个计算装置示意图,A、B是数据输入口,C是计算输出口,计算过程是由A、B分别输入自然数m和n,经计算后得自然数K由C输出,此种计算装置完成的计算满足以下三个性质:
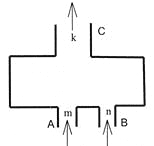
(1)若A、B分别输入1,则输出结果为1;
(2)若A输入任何固定的自然数不变,B输入自然数增大1,则输出结果比原来增大2;
(3)若B输入任何固定的自然数不变,A输入自然数增大1,则输出结果为原来的2倍。
试问:(1)若A输入1,B输入自然数4,输出结果为 。
(2)若B输入1,A输入自然数5,输出结果为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
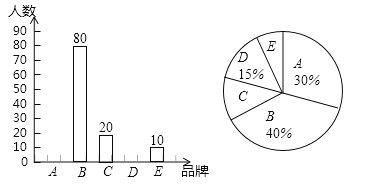
【题目】“共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
(1)求出本次参与调查的市民人数;
(2)将上面的条形图补充完整;
(3)若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩托单车出行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用“=”、“>”、“<”填空
![]()
![]() ; 6+3
; 6+3 ![]() ;
;![]()
![]() ;7+7
;7+7 ![]() ;
;
(2)由(1)中各式猜想a+b与![]() 的大小,并说明理由.
的大小,并说明理由.
(3)请利用上述结论解决下面问题:
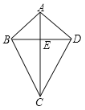
某同学在做一个面积为1800cm2,对角线互相垂直的四边形风筝时,求用来做对角线的竹条至少要多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们规定:点![]() 关于“
关于“![]() 的衍生点”,
的衍生点”,![]() ,其中
,其中![]() 为常数且
为常数且![]() ,如:点
,如:点![]() (
(![]() ,
,![]() )关于“
)关于“![]() 的衍生点”,即
的衍生点”,即![]() ,即
,即![]() .
.
(1)求点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() 的坐标;
的坐标;
(2)若点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,点
,点![]() 关于“
关于“![]() 的衍生点”
的衍生点” ![]() ,且线段
,且线段![]() 的长度不超过线段
的长度不超过线段![]() 长度的一半,请问:是否存在
长度的一半,请问:是否存在![]() 值使得
值使得![]() 到
到![]() 轴的距离是
轴的距离是![]() 到
到![]() 轴距离的
轴距离的![]() 倍?若存在,请求出
倍?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
根据城市规划设计,某市工程队准备为该城市修建一条长4800米的公路.铺设600米后,为了尽量减少施工对城市交通造成的影响,该工程队增加人力,实际每天修建公路的长度是原计划的2倍,结果9天完成任务,该工程队原计划每天铺设公路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足![]() +(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
+(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
(1)求出点A,B的坐标;
(2)如图2,若DB∥AC,∠BAC=a,且AM,DM分别平分∠CAB,∠ODB,求∠AMD的度数;(用含a的代数式表示).
(3)如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
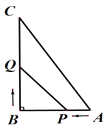
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com