
����Ŀ����ƽ��ֱ������ϵ�У���֪��A��a��0����B��b��3����C��4��0����������![]() +��a��b+6��2��0���߶�AB��y���ڵ�F����D��y���������ϵ�һ�㣮
+��a��b+6��2��0���߶�AB��y���ڵ�F����D��y���������ϵ�һ�㣮
��1�������A��B�����ꣻ
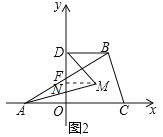
��2����ͼ2����DB��AC����BAC��a����AM��DM�ֱ�ƽ�֡�CAB����ODB�����AMD�Ķ��������ú�a�Ĵ���ʽ��ʾ����
��3����ͼ3�����������Ƿ����һ��P��ʹ�á�ABP������͡�ABC�������ȣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��A����3��0����B��3��3������2����AMD��45��+![]() a����3������.
a����3������.
��������
��1�����ݷǸ��������ʵõ�����a��b�Ķ�Ԫһ�η����飬Ȼ����⼴�ɣ�
��2������M��MN��DB����y���ڵ�N������ƽ���ߵ�������֤��AMD����AMN+��DMN���ٸ��ݽ�ƽ���ߵĶ����������ɵý⣻
��3�����ڣ���F��0��t��������S��AOF+S��BOF��S��AOB�����F�����꣬�ٷ�P����y���ϣ���x������������������ۼ���.
�⣺��1����![]() +��a��b+6��2��0��
+��a��b+6��2��0��
��a+b��0��a��b+6��0��
��a����3��b��3��
��A����3��0����B��3��3����
��2����ͼ2������M��MN��DB����y���ڵ�N��
���DMN����BDM��
����DB��AC��
��MN��AC��
���AMN����MAC��
��DB��AC����DOC��90����
���BDO��90����
����AM��DM�ֱ�ƽ����CAB����ODB����BAC��a��
���MAC��![]() a����BDM��45����
a����BDM��45����
���AMN��![]() a����DMN��45����
a����DMN��45����
���AMD����AMN+��DMN��45��+![]() a��
a��
��3�����ڣ�
����OB����ͼ3��

��F��0��t����
��S��AOF+S��BOF��S��AOB��
��![]() 3t+
3t+![]() t3��
t3��![]() ��3��3�����t��
��3��3�����t��![]() ��
��
��F��������0��![]() ����
����
��ABC�������![]() ��7��3��
��7��3��![]() ��
��
��P����y����ʱ����P��0��y����
��S��ABP��S��APF+S��BPF��
��![]() |y��
|y��![]() |3+
|3+![]() |y��
|y��![]() |3��
|3��![]() ��
��
���y��5��y����2��
����ʱP������Ϊ��0��5����0����2����
��P����x����ʱ����P��x��0����
��![]() |x+3|3��
|x+3|3��![]() ��
��
���x����10��x��4��
����ʱP������Ϊ����10��0����
���Ͽ�֪�������������ĵ�P��������Ϊ��0��5����0����2����10��0����


 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д� ��ѧ�����ϵ�д�
��ѧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
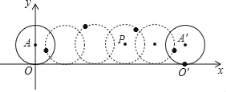
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��뾶Ϊ1��Բ��ԭ�������x�����������һ�ܣ�Բ��һ����ԭ��O�����O�䣬Բ��Ҳ�ӵ�A�����A�䣮
��1����O��������� ����A��������� ��
��2������P��Բ�ڹ���������Բ�ľ�����ijһλ�ã����Ե�P����O����O��Ϊ����������ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�EΪ�Խ���BD���ӳ�����һ�㣮

��1����֤��AE=CE��
��2����BC=6��AE=10����BAE=120����BE�ij�����ֱ��д��DE�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڸ�����һ��ƽ���ı���ֽƬ�ϰ����²���������AC����AC�Ĵ�ֱƽ����MN�ֱ�AD��AC��BC��M��O��N������AN��CM�����ı���ANCM�ǣ�������

A. ���� B. ���� C. ������ D. ���ж�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺���ǰ�![]() ��Ϊ��������ʽ���涨�������㷨��Ϊ
��Ϊ��������ʽ���涨�������㷨��Ϊ![]() ��ad��bc�����磺
��ad��bc�����磺![]() ��2��5��3��4����2��
��2��5��3��4����2��
��1����գ���![]() ��0����x���� ����
��0����x���� ����![]() ��0����x��ȡֵ��Χ�� ����
��0����x��ȡֵ��Χ�� ����
��2��������������m��n���㣬1![]() ��3����m+n��ֵ��
��3����m+n��ֵ��
��3�������������Ǹ���x��y��![]() ��
��![]() ��k��1����ʵ��k��ȡֵ��Χ��
��k��1����ʵ��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������
����![]() �ķ�����
�ķ�����
![]() �Ľ�Ϊ��
�Ľ�Ϊ�� ![]() ��
�� ![]()
![]() ���ɱ���Ϊ
���ɱ���Ϊ![]() ���Ľ�Ϊ��
���Ľ�Ϊ�� ![]() ��
�� ![]()
![]() �Ľ�Ϊ��
�Ľ�Ϊ�� ![]() ��
�� ![]()
![]() �Ľ�Ϊ��
�Ľ�Ϊ�� ![]() ��
�� ![]()
��������
�������ϲ��Ͻ������������
��1���ٷ���![]() �Ľ�Ϊ ��
�Ľ�Ϊ ��
�ڷ���![]() �Ľ�Ϊ ��
�Ľ�Ϊ ��
��2�������![]() ������
������
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ��壺��һ���ڱ���ȵ��ı��ν��������ڱ��ı��Ρ���

��1����֪����ͼ1���ı���ABCD�Ķ���A��B��C���������ϣ����������µ�5![]() 7�������л���3����ͬ��״�ĵ��ڱ��ı���ABCD��Ҫ��D������������
7�������л���3����ͬ��״�ĵ��ڱ��ı���ABCD��Ҫ��D������������
��2����ͼ2������ABCD�У�AB=![]() ��BC=5����E��BC���ϣ�����DE��AF
��BC=5����E��BC���ϣ�����DE��AF![]() DE�ڵ�F����DE=
DE�ڵ�F����DE=![]() CD���ҳ�ͼ�еĵ��ڱ��ı��Σ�
CD���ҳ�ͼ�еĵ��ڱ��ı��Σ�
��3����ͼ3����Rt![]() ABC�У�
ABC�У�![]() ACB=90����AB=4��AC=2��D��BC���е㣬��M��AB����һ�㣬���ı���ACDM�������ڱ��ı�����ʱ����BM�ij���
ACB=90����AB=4��AC=2��D��BC���е㣬��M��AB����һ�㣬���ı���ACDM�������ڱ��ı�����ʱ����BM�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
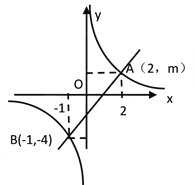
����Ŀ����ͼ��һ�κ�����ͼ���뷴����������ͼ���ཻ��A��B����.
��1������ͼ�е�����������������һ�κ����Ľ���ʽ��
��2������ͼ��ֱ��д��һ�κ�����ֵ���ڷ�����������x��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ľ�����̵ĺ�������գ�����������ע������
.��ͼ����֪��A=��F����C=��D����˵��BD��CE.

�⣺�ߡ�A=��F(��֪)
��AC��DF( )
���D=�� ( )
���ߡ�C=��D(��֪)
���1=��C(��������)
��BD��CE( )
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com