
【题目】阅读材料:
关于![]() 的方程:
的方程:
![]() 的解为:
的解为: ![]() ,
, ![]()
![]() (可变形为
(可变形为![]() )的解为:
)的解为: ![]() ,
, ![]()
![]() 的解为:
的解为: ![]() ,
, ![]()
![]() 的解为:
的解为: ![]() ,
, ![]()
…………
根据以上材料解答下列问题:
(1)①方程![]() 的解为 .
的解为 .
②方程![]() 的解为 .
的解为 .
(2)解关于![]() 方程:
方程:
①![]() (
(![]() )
)
②![]() (
(![]() )
)
【答案】(1)①![]() ,
, ![]() ;②
;②![]() ,
, ![]() ;(2)①
;(2)①![]() ,
, ![]() ;②
;②![]() ,
, ![]() .
.
【解析】试题分析:(1)①令第一个方程中的a=2即可得到答案;
②把(x-1)看成一个整体,利用第一个方程的规律即可得出答案;
(2)①等式两边减去1,把(x-1)和(a-1)分别看成是整体,利用第三个方程的规律即可得出答案;
②等式两边减去2,把(x-2)和(a-2)分别看成是整体,利用第二个方程和第四个方程的规律即可得出答案.
试题解析:
解:(1)①由第一个方程规律可得:x1=2,x2=![]() ;
;
②根据第一个方程规律可得:x-1=3或x-1=![]() ,
,
∴x1=4,x2=![]() ;
;
(2)①方程两边减1得:(x-1)+![]() =(a-1)+
=(a-1)+ ![]() ,
,
∴x-1=a-1或x-1=![]() ,
,
∴:x1=a,x2=![]() ;
;
②方程两边减2得:(x-2)+![]() =(a-2)+
=(a-2)+ ![]() ,
,
∴∴x-2=a-2或x-2=![]() ,
,
∴:x1=a,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】列方程解应用题
根据城市规划设计,某市工程队准备为该城市修建一条长4800米的公路.铺设600米后,为了尽量减少施工对城市交通造成的影响,该工程队增加人力,实际每天修建公路的长度是原计划的2倍,结果9天完成任务,该工程队原计划每天铺设公路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列![]() ,
, ![]() ,0,1,2,3这6个数中任取一个数记作
,0,1,2,3这6个数中任取一个数记作![]() ,放回去,再从这六个数中任意取一个数记作
,放回去,再从这六个数中任意取一个数记作![]() ,则使得分式方程
,则使得分式方程![]() 有整数解,且使得函数
有整数解,且使得函数![]() 的图象经过第一三四象限的所有
的图象经过第一三四象限的所有![]() 的值有( ).
的值有( ).
A. 2个 B. 4个 C. 5个 D. 8个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(a,0),B(b,3),C(4,0),且满足![]() +(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
+(a﹣b+6)2=0,线段AB交y轴于点F,点D是y轴正半轴上的一点.
(1)求出点A,B的坐标;
(2)如图2,若DB∥AC,∠BAC=a,且AM,DM分别平分∠CAB,∠ODB,求∠AMD的度数;(用含a的代数式表示).
(3)如图3,坐标轴上是否存在一点P,使得△ABP的面积和△ABC的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,AC=6,BC=8,现将△ABC沿直线AD折叠,使AC落在斜边AB上,且C与点E重合,则AD的长为________.
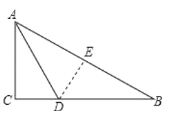
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )

A.(0,﹣4)B.(﹣2,0)C.(2,4)D.(﹣2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①已知:△ABC中,BC=m,∠A=60°.问满足此条件的三角形有多少个?它们的最大面积存在吗?若存在求出最大面积,并回答此时三角形的形状;若不存在,请说明理由.

②有一个正方形的养鱼塘,四个角各有一棵大树.生产队设想把鱼塘扩大,使它成为一个面积最大的正方形,而又不把树挖掉,这一设想能否实现?若能,请你设计画出图形,并证明此时面积最大.若不能,请说明理由.

③上问题推广,有一个正五边形的养鱼塘,五个角各有一棵树,要扩大使它成为面积最大的正五边形,而又不把树挖掉,可以吗?画图说明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com